Sarah Hofmann, UGA, EMAT 6680, Summer 2006, Assignment 7

Sarah Hofmann
EMAT 6680
Summer 2006
Assignment 7

What I found interesting or most helpful was the way this assignment used tangent circles to get the students to recognize the patterns and constructions of hyperbolas and ellipses. Unlike parabolas, which get heavy attention in all algebra classes and above, the hyperbollic and elliptic conic sections are often introduced and then quickly reduced to their equations. Students don't spend much time thinking about their construction as the locus of points that can be drawn. The concept of the hyperbola and ellipse as a locus of points is hammered home here when we look at the proofs for whether the locus of the tangent circles center are in fact hyperbolic and elliptic as we hope the students would suspect. It also gives the students a reason to study hyperbolas and ellipses. These conic sections are not as readily seen in nature as the parabola (or circle) and it's a nice way to give the shapes purpose. Below we have presented our proofs for when the locus of the centers of tangent circles are ellipses and parabolas.

Proof 1: We must show that when a circle is interior to another circle and the small circle is exterior to the tangent circle, the locus of the centers of their tangent circle is an ellipse (in fact the cases where there is a small circle interior to a large circle and two intersecting circles are similar proofs).

We know that an ellipse is the locus of all points x whose sum of the distances r1 from a fixed point a and r2 from a fixed point b is constant. So we must show for any tangent circle, the sum of the distances r1 from the center of the small circle to the center of the tangent circle and r2 from the center of the large circle to the center of the tangent circle is constant.

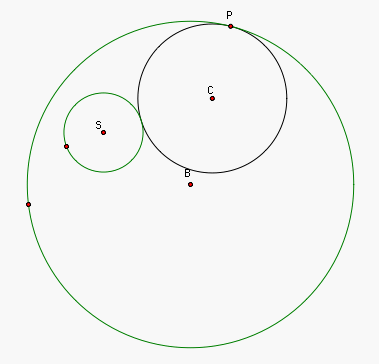
We will begin by drawing the above case where there is a small circle interior to a large circle, a point on the large circle, and we will consider the tangent circle where the small circle is external to the tangent circle. Let S be the center of the small circle, B the center of the big circle, P the point of tangency on the big circle, and C the center of the tangent circle, as shown in the below picture.

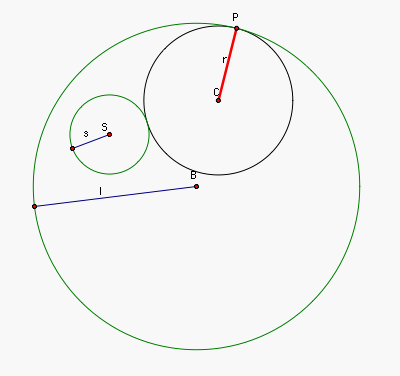
Let s be the length of the radius of the small circle, l the length of the radius of the large circle, and r the length of the radius of the tangent circle, as shown below.

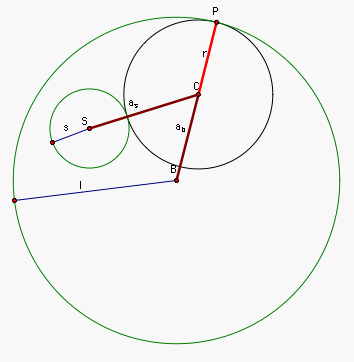
Let as be the distance from the cener of the small circle to the center of the tangent circle, and let ab be the distance from the center of the large circle to the center of the tangent circle, as shown below.

Now, from the above picture and the definitions of how we attained the tangent circle, we can see the following facts.

as = s + r
ab + r = l

By solving the second equation for ab, we get

ab = l - r

Since we need to see if the sum of the distances from the center of the small circle to the center of the tangent circle (from S to C or as) and from the center of the large circle to the center of the tangent circle (from B to C or at) is constant, we need to consider

as + ab = (s + r) + (l - r) = s + l + r - r = s + l

But the radius of the small circle and the radius of the large circle (s and l) are constants, hence s + l is a constant. Therefore as + ab is a constant, which is the desired result. Threfore, the locus of points is an ellipse, as needed.

Proof 2: We must show that for two non-intersecting and non-concurrent circles, the locus of the centers of the tangent circles is a hyperbola.

We know that a hyperbola is the locus of all points x whose difference of distances between x and a foci point a and x and another foci point b is constant. So we can show that the locus of the centers of the tangent circles is an ellipse if we can show that the distance from the center of the tangent circle to the center of circle one minus the distance from the tagent circle to the center of circle two is constant.

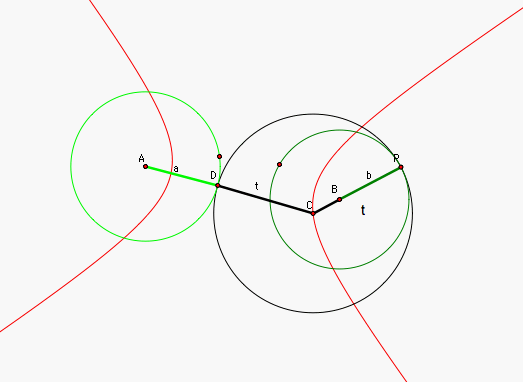
Let the center of circle one (light green) be A and its radius be of length a, the center of circle two (dark green) be B and its radius be of length b, the point of tangency on circle two be P, the center of the tangent circle (black) be C and the length of its radius be t, and the point of tangency between circle one and the tangent circle be point D, as shown in the below picture. The red represents locus of all points of the points C as P travels around circle two, which we are trying to show is a hyperbola.

From the above picture and from the construction of the tangent circle we can see:

dist(AC) = a + t
dist(CB) = t - b

So we can see

dist(AC) - dist(CB) = (a + t) - (t - b) = a + t - t + b = a + b

where a and b are constants. Therefore the difference of the distances from A to C and from C to B is a constant, as needed. Therefore the locus of centers of the tangent circles is a hyperbola, as needed.