Sarah Hofmann, EMAT 6680, Summer 2006, Assignment 8

Sarah Hofmann
EMAT 6680
Summer 2006
Assignment 8

I enjoyed the solution path that I took in completing task number 15, so that is the task I have chosen to write up. This was a fun problem to solve.

Problem 15: Find the triangle of minimum perimeter that can be inscribed inside of a given triangle.

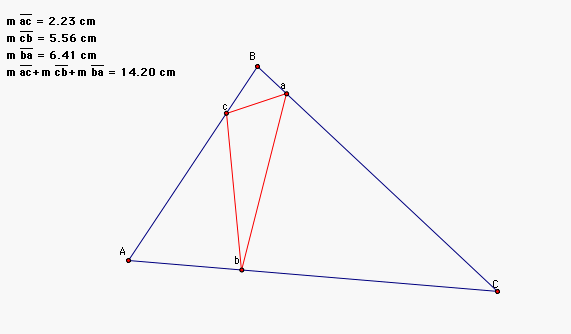
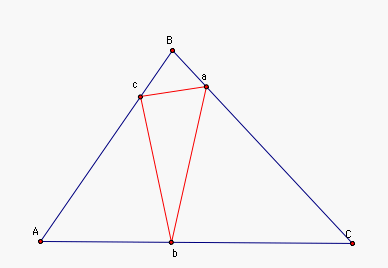
To begin this problem, I drew an acute triangle ABC and put points a,b, and c on the sides. I then created the triangle abc. Next I measured the lengths of segments ab, bc, and ca. Then I calculated their sum to find the perimeter. Finally I used the animation function and some movements by hand to find the approximate places where a, b, and c should be located to minimize the perimeter. Then I repeated the process to make sure that I indeed had the minimum perimeter. The following is a picture of my final results.

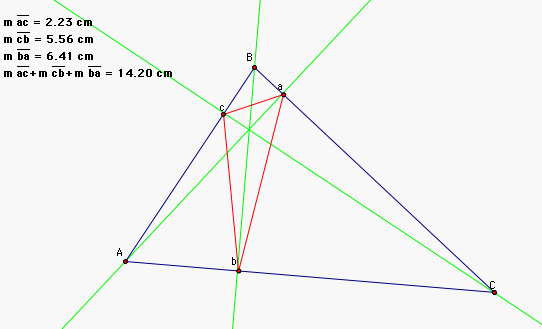
Now I needed to look at my results and come up with a hypothesis. It looks like if you connected B and b with a segment it would almost create a right angle with segment AC. Let's test this hypothesis by constructing those perpendicular lines, shown in green below.

A you can see, the approximated points a, b, and c all look very close to the intersections of the perpendicular lines and the segments. So we now have a conjecture that the triangle of minimum perimeter that can be constructed in a given triangle is the orthic triangle.

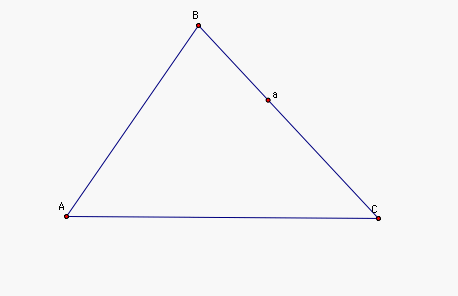
We begin by drawing triangle ABC and selecting a random point a on segment BC.

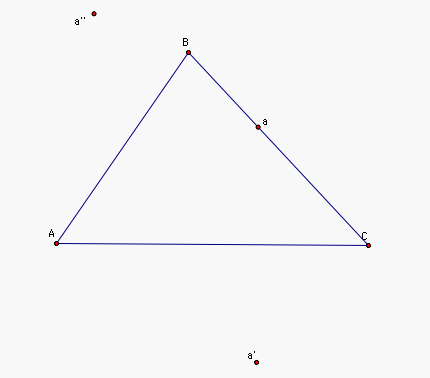
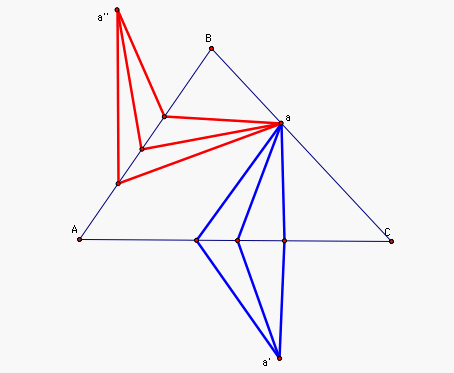
Next we will look at the reflections of point a about segment AC and AB. Call these points a' and a'' respectively.

Since a' is the reflection of a about AC, any point b on AC is equidistant from a and a'. Similarly, any point c on segment AB is equidistant from a and a'', as seen in the picture below.

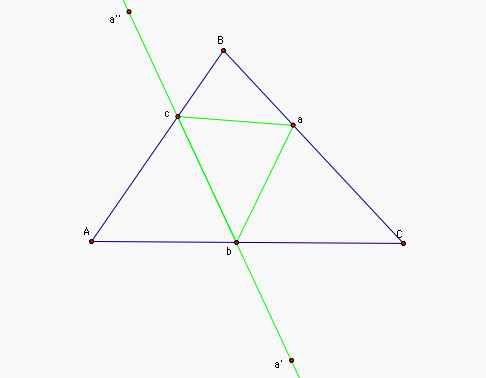
So any triangle abc with fixed vertex a has perimeter

perim(abc) = m(ab) + m(bc) + m(ca) = m(a'b) + m(bc) + m(ca'').

In order to minimize the perimeter of a hypothetical triangle abc which has one of its verticies fixed at a, we must minimize m(a'b) and m(a''c) at the same time, so the points b and c must lie on the line a'a''. So for any fixed point a on segment BC, the triangle of minimum perimeter is shown below.

A similar statement is true for a random "b" point or a random "c" point. So the triangle we are looking for must have this form in all three of its points.

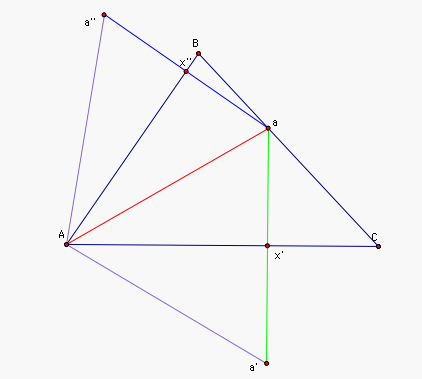
Now let us look at the picture below. Since a' is the reflection of a about AC we know that m(ax') = m(x'a) and m(Aa) = m(Aa') as segments. Thus angle aAx' equals angle a'Ax'. Similarly angle aAx'' equalse angle a''Ax''. Thus the m(a''Aa') = m(a''Ax'') + m(x''Aa) + m(aAx') + m(x'Aa') = 2m(x''Aa) + 2m(aAx') = 2m(BAC).

Thus the position of a on BC does not affect the measure of angle a'Aa''. The same statement can be made for points b and c. Thus all triangles that fit our hypothesis have the same angles. Thus all triangles that fit our hypothesis are similar.

The similar triangle with the shortest length a'a'' has the shortest m(Aa') = m(Aa). Thus the solution is true when Aa is as short as possible, which is when Aa is perpendicular to BC. Similarly Bb must be perpendicular to AC and Cc must be perpendicular to AB. Therefore, abc must be the orthic triangle as needed.