Sarah Hofmann
EMAT 6080
Summer 2006
Assignment 9
|
For assignment number 9, we
have chosen to explore problems 8 and 9 having to do with the Simpson
Line.
|
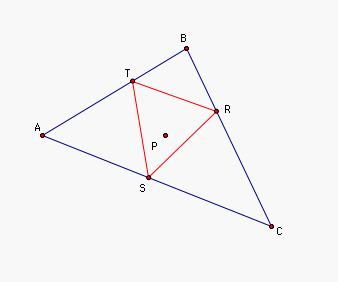
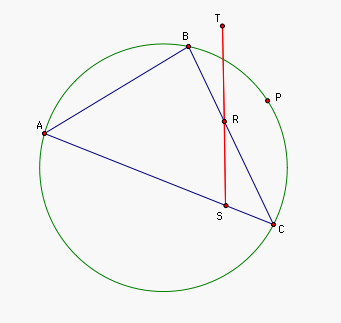
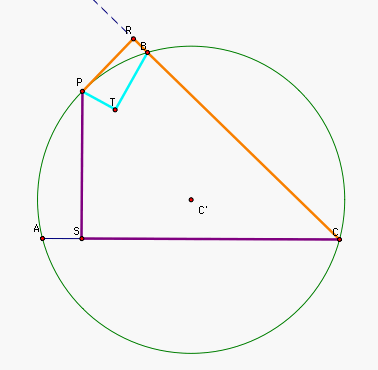
First we constructed a triangle ABC and a point P. Then we constructed the petal
triangle RST for triangle ABC and point P.
|
Problem 8 asked what happens
when the petal point P is one
of the verticies of triangle ABC.
We can see that in all three cases, the petal triangle appears to be
linear.
Let's try to prove the conjecture: If P
is a vertex of the triangle, then the petal triangle is linear.
|
Let ABC be a triangle, P a point, and RST the petal triangle for point P and triangle ABC, where R is on line BC, S
is on line AC, and T is on line AB, as shown below.
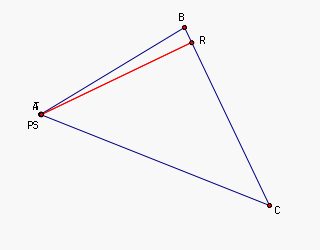
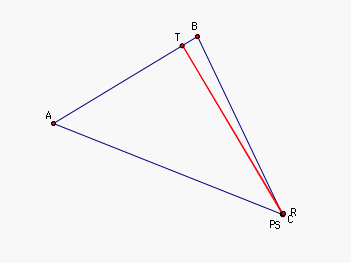
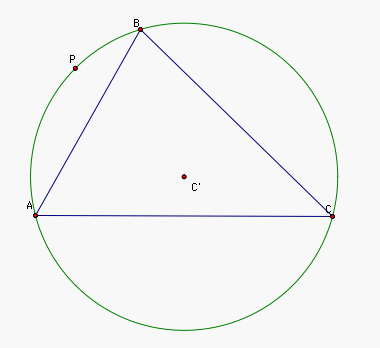
Suppose P = A. Then we can see that the
intersection of the line through A
perpendicular to line AB is A. So S = A.
The intersection of the the line through A perpendicular to the line AC is A. So T = A.
So, S = T. Thus RST = RTT = RT, which is a segment, as needed.
|
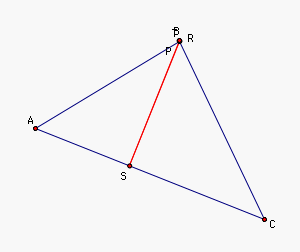
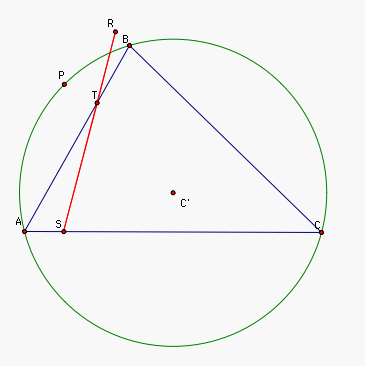
Problem 9 asks us to find all
points in which the petal triangle is a segment (this is called Simpson
Line). Since all three points A,
B, and C are points where the petal
triangle is linear, and all three points A, B,
and C are on the
circumcircle. The circumcircle would be a good place to look to
find all points in which the petal triangle is linear. Lets try.
Looks like it worked! Let's see if we can prove it.
|
Conjecture:
The petal triangle is colinear if and only if, P is on the circumcircle of ABC.
Proof:
|
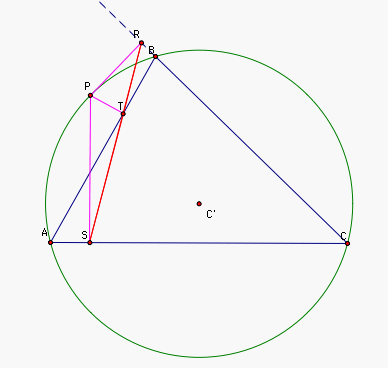
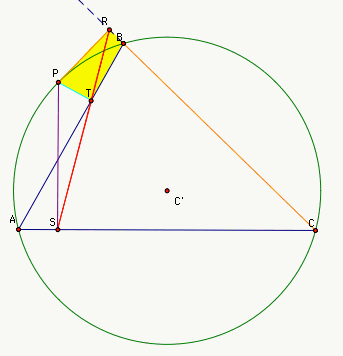
Let ABC be a triangle, C' its circumcenter, and P a point on its circumcircle.
|
Construct the pedal triangle RST from the perpendicular
intersections of lines through point P
with the segments of ABC.
|
From our construction of RST we know that segment PS is perpendicular to line AC, PT
is perpeendicular to AB, and PR is perpendicular to BC.
|
Since the above segments are
perpendicular to the mentioned lines we can see
angle( PTB) = 90 degrees
angle( PRB) = 90 degrees
angle( PSC) = 90 degrees
angle( PRC) = 90 degrees
|
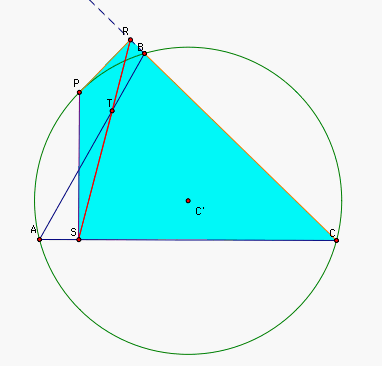
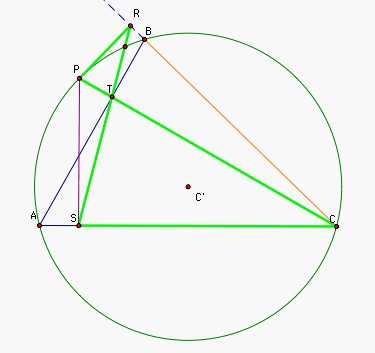
So PTBR and PSCR are cyclic quadrilaterals
(quadrilaterals whose opposite angles are equal - 90 degrees).
We know PTBR and PSCR are cyclic quadrilaterals if
and only if
angle( PRT) = angle( PBT)
angle( PRS) = angle( PCS)
|
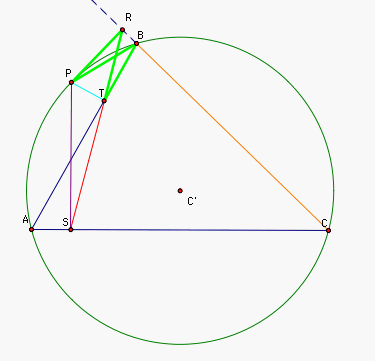
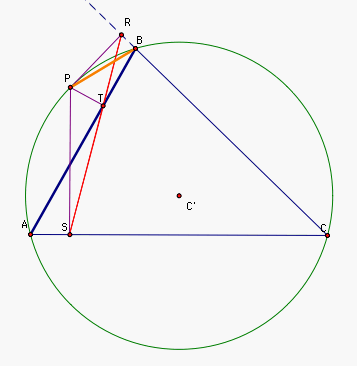
We finally note that since
points A, B, and T all lie on the same segment,
angle( PBT) = angle( PBA)
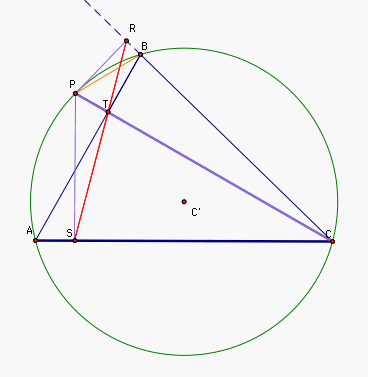
Similarly we can see that
angle( PCA) = angle( PCS)
|
Using the above equalities we
can now see the following
angle( PRT) = angle (PRS).
So R,T,
and S must be collinear, as
needed.
|