Problem #11

Consider any triangle ABC. Find a construction for a point P such that the sum of the distances from P to each of the three vertices is a minimum.

Let’s explore the triangle ABC below with the indicated medians:

INITIAL HYPOTHESES

1) The point P would be inside the triangle, because any point outside the triangle would be equidistant to the nearest vertex(es) inside and would also have a greater distance from the farthest vertex(es). The extra distance will yield a greater sum than what is required.

2) The point P is a center of a triangle and is equidistant from each vertex.

Let’s consider four specific centers for a triangle:

Centroid (G)- the common intersection of the three medians, which are formed from segments, constructed using a vertex and the midpoint of the opposite side.

Orthocenter (H)- The common intersection of the three lines containing the altitudes.

Circumcenter (C)- is the point in the plane that is equidistant from the three vertices of the triangle.

Incenter (I) is the point on the interior of the triangle that is equidistant from the three sides.

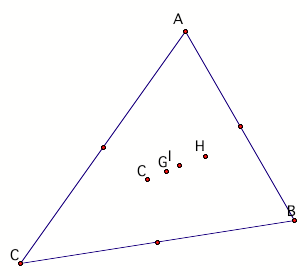
The points C, G, I, and H are all centers of the acute triangle ABC. Because all of the angels at each vertex are acute, all of the centers are located within the interior of the triangle.

Now let’s reconstruct the perpendicular bisectors which will have a common point C which is the Circumcenter (C).

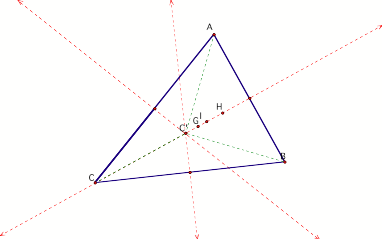
The red dashed lines indicate the perpendicular bisectors to the sides of the triangle. The segments AC’, CC’, and BC’ which are represented by the green dashed lines, are all congruent. Since C is equidistant to all of the vertices, then C’ is my point ‘P’ where the sum of the segments from that point to the vertices are a minimum.

Return