
Damarrio C. Holloway
Assignment #7
Loci of Centers
Problem #4:
Discuss the loci of the centers of the tangent circles for all cases you
construct.
The investigation begins with the problem of constructing a
tangent circle (Blue) to two given circles (Green). We first discover the center of the desired circle is
collinear to the line formed by the center and the specified point ÔRŐ on the
given circle.
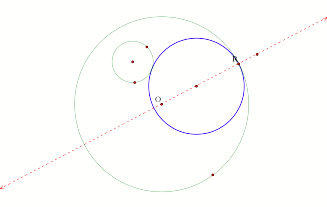 Figure
1
Figure
1
Figure 2 below shows the construction of a traced point,
which is the center of the desired tangent circle. This trace (Red) displays the location or loci of all
centers of the different circles (Blue) that are tangent to the two given
circles (Green).
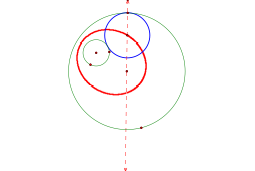
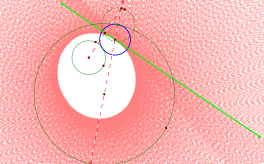
Figure
2 Figure
3
Figure 3 displays the elliptical shape, which are the loci
of all of the centers. The green
line in the picture traces an envelop of line, always tangent to the loci of
the centers-ellipse.
Now lets discover another set of circles tangent to the two
given circles by using similar, but different tactics.
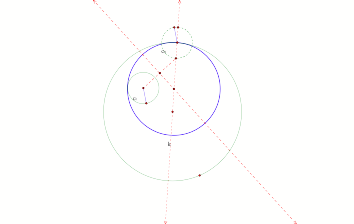 Figure
4
Figure
4
In Figure 4, the small internal circle has the same radius
as the dashed circle with center on the designated point on the larger
circle. The first tangent circle
was formed by the perpendicular bisector of the segment connecting the center
of the smaller given circle and the external point of the copied dashed circle that is collinear the center of the
large given circle an the designated point. The center of the above tangent circle (Blue) still lies on
the line k, containing the center and designated point of the larger given
circle. Instead of using the
external intersection point on the copied circle, we use the segment formed by
the internal intersection of line k on the dashed circle c2 and the center of
the smaller green circle c1. A
perpendicular bisector was form through the midpoint of the segment, creating a
desired intersection with line k, which is the center of our tangent circle.
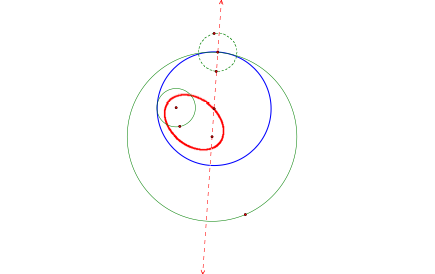
Figure
5 Figure
6
Figure 5 and Figure 6 show the path the centers will travel
when the tangent circle approaches different tangent points on the given
circles. This locus of centers
again forms an ellipse.
We have shown tangent circles for two given circles, where a
smaller circles lies within the interior of another circle, not sharing the
same center. Now letŐs explore two
different tangent circles for where the given circles intersect.
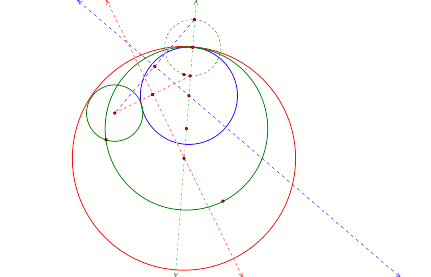 Figure
6
Figure
6
In figure 6, above, the given circles are again in green where they intersect at two different points. They have two different tangent circles: an interior tangent circle in Blue and an exterior tangent circle in Red. As the earlier examples, the centers of the tangent circles are collinear to the line formed by the center of the large given circle and the designated point of intersection.
LetŐs look at the locus of the centers of the tangent circles.
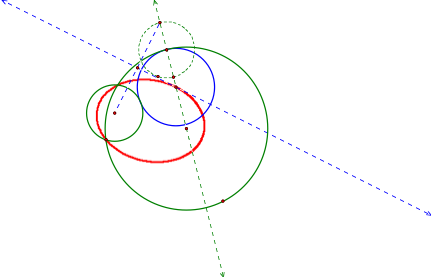
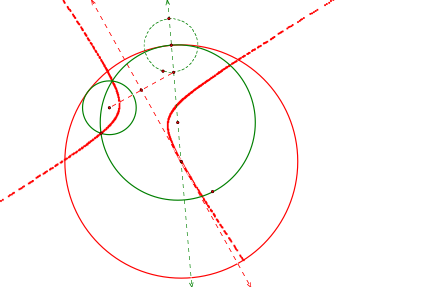
In Figure 7, the locus of centers for the tangent circles is
an ellipse. In Figure 8, the locus
of centers is in a parabolic shape.
Click on the picture titles to animate objects in GSP. The designated tangent point on the
given circle should be the animated point, while tracing the centers of the
tangent circles.
Return