Altitude Sums of
Inscribed Triangle
By: Damarrio C. Holloway
Assignment #8
Problem 11.
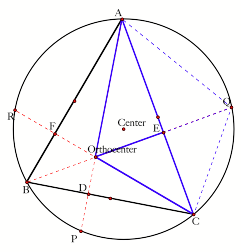
Construct any acute triangle ABC and its circumcircle. Construct the three altitudes AD, BE,
and CF. Extend each altitude to its intersection with the circumcircle at
corresponding points P, Q, and R.
The problem continues to find we are required to find the sum of the ratios of:
AP/AD + BQ/BE + CR/CF
LetŐs separate the figure into several triangles using the different sides of the inscribed triangle ABC.
1. Expression AP/AD:
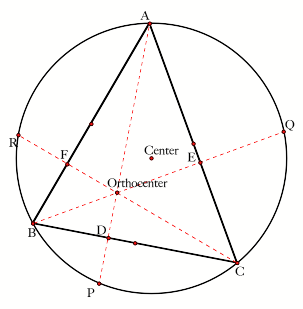
The length of AD is the altitude from the vertex A to the opposite side of BC. The length of AP includes that altitude plus the segment of DP. If we form two triangles using the Orthocenter (H), Triangle BHC and the point on the circle Triangle BPC, we see that they have two things in common, the have the same base BC and congruent heights HD and DP as seen in the picture below.
 Thus, AP = AD + PD
Thus, AP = AD + PD
2. Expression BQ/BE:
Using a similar method, we will now focus on the construction
of two other triangles both containing the side AC. As shown below, the altitude BE is extended to the point Q
on the circle, forming the two triangles:
Triangle CHA and Triangle CQA.
We see that they have equal heights of HE and EQ, with a common side
AC.
3. Expression CR/CF:
Let us now look at the triangles formed using a common side AB. The altitude CF, formed on Triangle ABC, is extended to the point R on the circle. The triangles AHB and RB are displayed below, with equal heights (altitudes) HF and FR, respectfully.
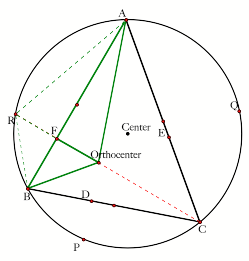 Thus, CR
= CF + FR
Thus, CR
= CF + FR
Going back to our original equation of: AP/AD + BQ/BE + CR/CF, we can now use substitution from our previous illustrations.
Now, (AD + PD)/AD + (BE + QE)/BE + (CF + RF)/CF
= {1 + (PD/AD) + {1 + (QE/BE)} + {1 + (RF/CF)}
= 3 + (PD/AD) + (QE/BE) + (RF/CF)
These three quotients are the heights/altitudes of their
respective base. Since the area of
a triangle is ½ bh, then we can multiply these heights (h) by their
respective bases (b) and ½.
= 3 + (PD/AD)(BC/BC) +
(QE/BE)(AC/AC) + (RF/CF)(AB/AB)
Total Area of ABC
(The ½ cancels)
= 3 + 1
Therefore, the sum of the quotient: AP/AD + BQ/BE +
CR/CF = 4.
Return