Where Are You Pedal Triangle?

By: Damarrio C. Holloway

Summer 2006

If we take triangle ABC and P as any point in the plane, we can construct perpendiculars from point P to the sides (extended if necessary) of triangle ABC. The intersections of perpendiculars will form a triangle called the Pedal Triangle. This point P is then called the Pedal Point.

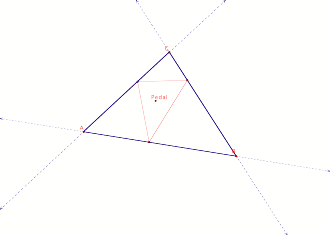Sample Pedal Triangle

What if pedal point P is the Orthocenter of triangle ABC, where the orthocenter is inside the triangle?

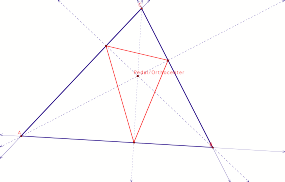Pedal as interior Orthocenter

When pedal point P is the orthocenter located within triangle ABC, the vertices of the Pedal Triangle are on the feet of the altitudes of the sides of triangle ABC.

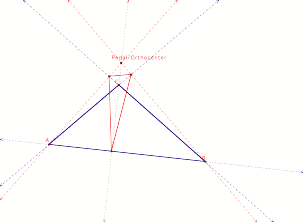P as Exterior Orthocenter

When we make the triangle ABC obtuse, the orthocenter is located outside the triangle. When the pedal point is the exterior orthocenter, the vertices of the Pedal Triangle are perpendicular intersections of the sides of triangle ABC (with extensions) and the altitudes. The pedal triangle now becomes the Orthic triangle.

What if the pedal point P is the centroid or the incenter of triangle ABC?

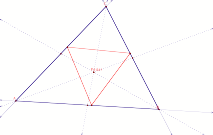Pedal point as Centroid 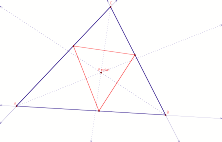Pedal point as the incenter

Nothing special occurs when pedal point P is the intersection of the angle bisectors or the common intersection of the medians.

What if the pedal point P is the Circumcenter of Triangle ABC?

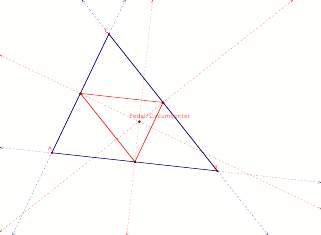P as Interior Circumcenter

When the pedal point P is the interior circumcenter, the vertices of the pedal triangle are the medians of the sides of triangle ABC. The segments connecting the three medians are displayed as the Pedal Triangle. Therefore, by definition, the Pedal Triangle becomes the Medial Triangle.

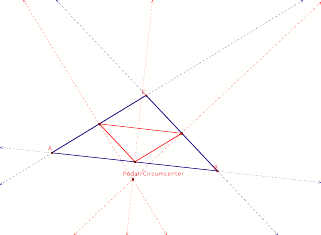P as Exterior Circumcenter

An obtuse triangle will yield an exterior Circumcenter. When the pedal point P is the circumcenter, the Pedal Triangle is still a Medial Triangle. In both cases, the Pedal/Medial Triangle creates 4 congruent interior triangles.

Pedal Point P as the center of the Nine Point Circle

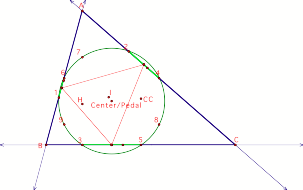
The vertices of the pedal triangle are the midpoints of the segments between the feet of the altitudes and the midpoints on triangle ABC.

What if P is on the side or vertex of the triangle ABC?

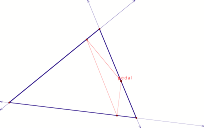
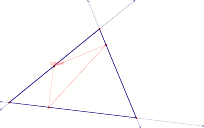
Whenever the pedal point is on any side of the given triangle, it becomes a vertex of the pedal triangle.

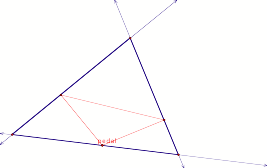
Also, in each figure, when the pedal point is on any side (as a vertex of the pedal triangle), it forms three interior triangles. The three interior triangles are all acute with the triangles adjacent to the pedal point are right triangles.

Return