Assignment 9

 

This assignment will bring us into connection with pedal triangles and pedal points. First let’s examine what a pedal point and triangle is by this sketch below:

 

 

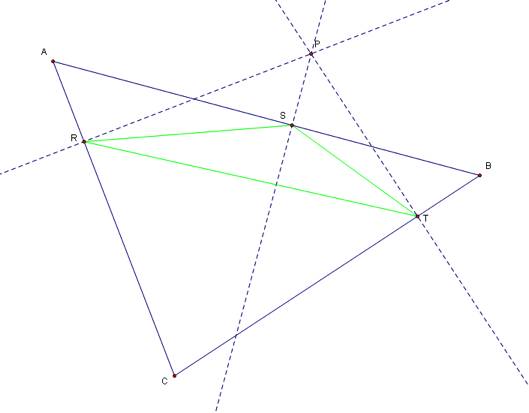
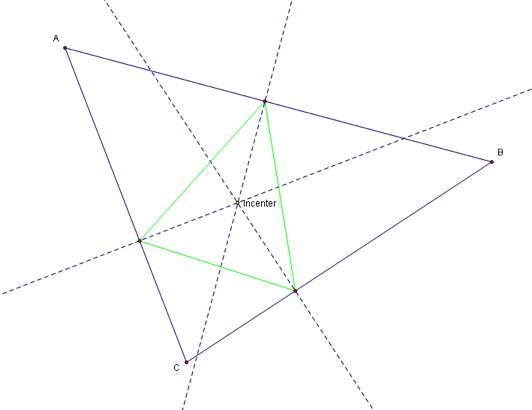
Here we have any triangle ABC and any point in the plane P, if we draw perpendicular lines from P to all three sides of the triangle, we get three intersections: R, S and T. Then we connect these three point using segments to form the pedal triangle and point P now becomes the pedal point. So what we are attempting to do in this assignment is look at the pedal triangle when the pedal point P is a particular point in the plane, not any point in the plane. So if point P is the incenter, we have constructed

 

 

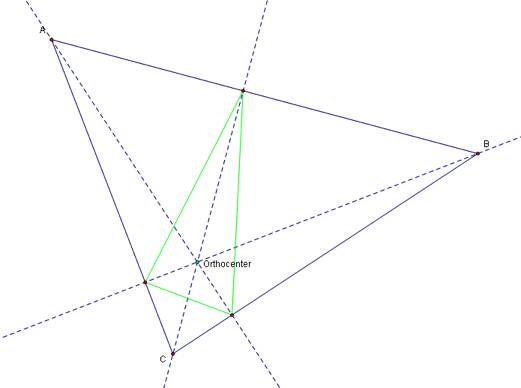
Now if the pedal point is the orthocenter we construct

 

 

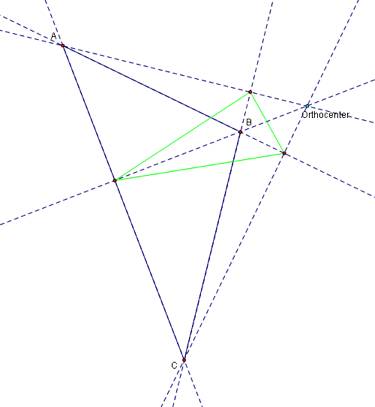
But what if the orthocenter is outside of triangle ABC? Then we have this construction:

 

 

Now let’s examine the pedal point being the circumcenter:

 

 

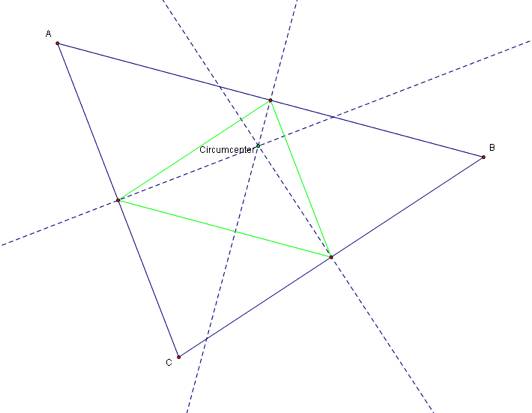
Yet if the circumcenter is outside of triangle ABC we get a different looking triangle:

 

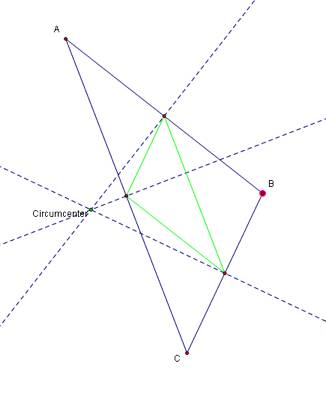
We can see by the sketches that the pedal triangle remains inside of triangle ABC despite whether or not the circumcenter is inside or outside of the original triangle but if the orthocenter is outside the original triangle then the pedal triangle is as well. Now lets examine the pedal point being the center of a nine point circle, then the sketch would look like below:

 

 

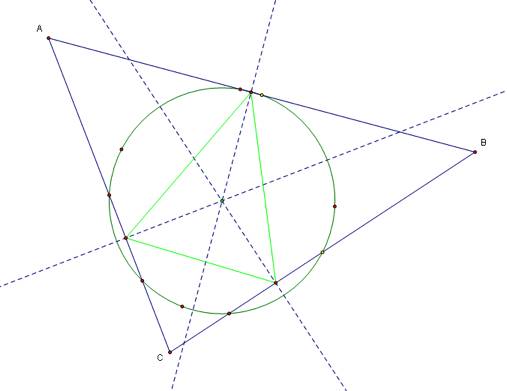
Finally lets explore the effects on the pedal triangle when the pedal point is located on a side of triangle ABC and at one of the vertices.

 

 

 

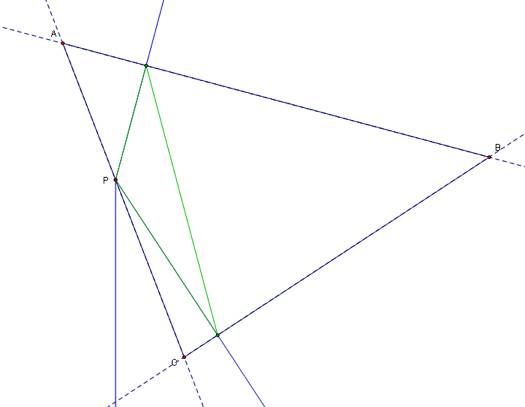
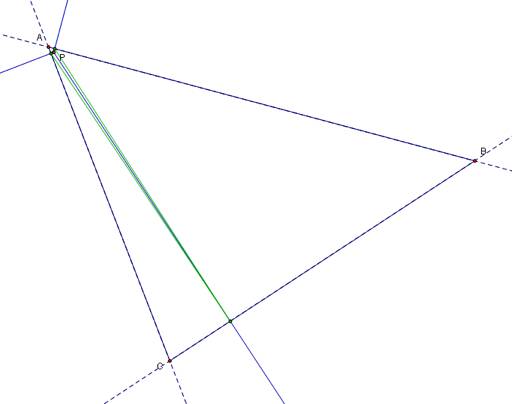
In the last sketch, the pedal point is not on the vertice A but you can examine that as P moves closer to A then the pedal triangle becomes increasingly smaller, therefore if the pedal point and a vertice were to be the same point, then there would not exist a pedal triangle. As we have seen when P is a specific point in the plane then the pedal triangle reacts differently to each individual point as well as the location of the point, i.e. inside or outside of the original triangle.