Christa Marie Nathe                                   Parabola Shifts

 

 

In this investigation we are going to construct a series of graphs based on the equation y=ax2 + bx + c.  There will be different values for a, b and c which are any rational number.  The first set of graphs reflects the following equations where the value for a is varied, while the others remain constant.

                                                                 

       y= 1x2+2x+3

 

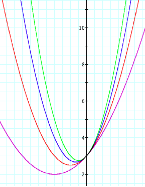
       y= 2x2+2x+3

 

       y= 3x2+2x+3

 

       y= 4x2+2x+3

 

 

 

It is obvious from the graph that when the value for a changes, the graph is altered. As the value for a increases, the parabola becomes thinner than its predecessor. If the values for a are negative the parabolas are reflected over the x-axis.

 

                                                                                                                             y= -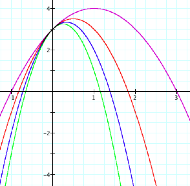1x2+2x+3

 

   y= -2x2+2x+3

 

   y= -3x2+2x+3

 

   y= -4x2+2x+3


 

 

 

 

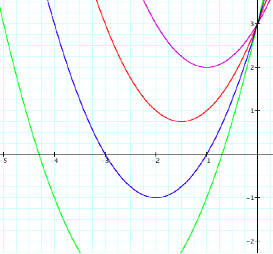
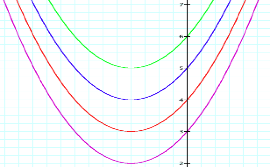
The following graphs reflects the various values of b, while a and c are kept constant. The graph expands as the value of b increases and interestingly pulls to the left. We can expect that if the values for b were negative that the parabola would expand, but pull to the right. As we observe, this is the case.

 

 y=x2+2x+3      y=x2+2x+3      y=x2+2x+3      y=x2+2x+3                    y=x2-2x+3        y=x2-2x+3        y=x2-2x+3      y=x2-2x+3                   

 

 

 

 

                 

 

 

 

 

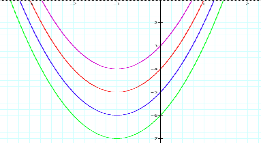
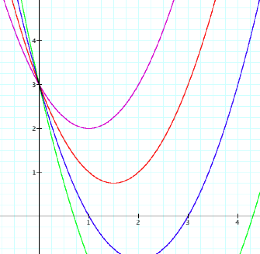
Now we will look at the graphs of the equation where the value for c is changed, both positive and negative.  As you have observed from the previous graphs, it would seem that the c value anchors the graph  to a y-intercept. As we change c, while a and b remain constant one could predict the shifts of the graphs.

 

 

 

y=x2+2x-3        y=x2+2x-4       y=x2+2x-5       y=x2+2x-6                   y=x2+2x+3       y=x2+2x+4      y=x2+2x+5      y=x2+2x+6      

                                                                                                                                                                                                                                                                                                                                            

 

As we have observed in this investigation, the coefficients  a, b and c have direct bearing on the graph.  Realizing these implications allows one to understand the functions of the quadric equation.