Christa Marie Nathe
Quadric Equations and Roots
In this investigation we will
look at the basic quadric equation ax2+bx+c=y and the patterns of
roots that arise from graphing said equation. The values for a, b and c all play a vital role in the graphical
representation of the equation. Below one will find several graphs of the
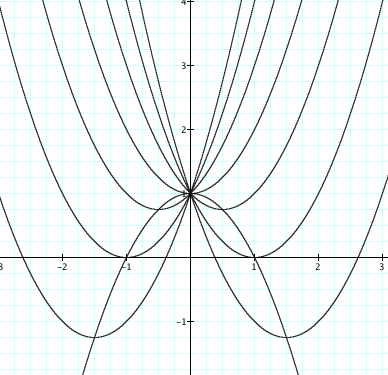
equation y=x2+bx+1, where the values of b are changed. Looking at the graph, which values of b
correspond to which parabola?
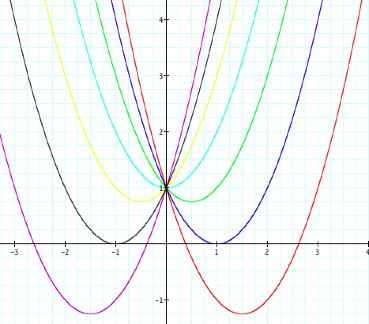
When b is negative
3(red), 2(blue) and 1(green) the parabola lies in the first and fourth
quadrant. Alternatively, when b
is positive 3(pink), 2(gray) and 1(yellow) the parabola occupies the second and
fourth quadrants. What happens when b is zero? That is the graph, which is represented by the light blue
parabola. It does not cross the
x-axis into another quadrant. All
of these graphs have one characteristic in common; they all cross the y-axis at
the same point. The value of c=1
does not change, and determines the point where the parabola will cross the
y-axis.
Now that we have identified which b value represents which parabola, lets look at where
those graphs cross the x-axis and its significance. Where the graph crosses the x-axis is where there is a root
of the equation. For which value of b does the graph cross the x-axis more than once? When b is -3 or 3. Therefore there exists two real roots
positive and negative respectively.
What happens when b is -2
and 2? The parabola is tangent to the x-axis and hence has only one real
root. When are there no real roots
for the equation graphed? Yes, when b is -1 or 1.
Looking at the vertices of the parabolas above, what
significance do they relay? If the vertices are traced and connected they will
form an upside down parabola where y=-x2+1 as depicted below.