Tangent Tango
by
Christa Marie Nathe
Presented with the
problem where we are given two circles and a point on one of the circles, and
we want to construct a circle tangent to the two circles with one point of
tangency being the chosen point. The
figure below will be the construction we will use to derive the tangent circle.
Specifically what our objectives are is to find one common point to the outside of the small circle and one common point to the interior of the large circle that will be yield the radius of the desired tangent circle.
In order to proceed
in creating the desired tangent circle, we must first acknowledge that the
center of the preferred tangent circle will be located on a line going through
the center of the large circle.
By marking the radius of the small circle we can make an identical circle at the apex of the large circle where the center point is on the large circle, as shown below.
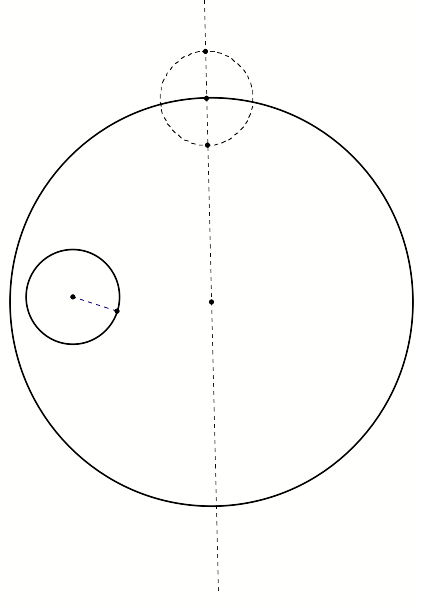
The next step is to
connect the center point of the small internal circle to the top of the small
dashed circle and plot its midpoint.
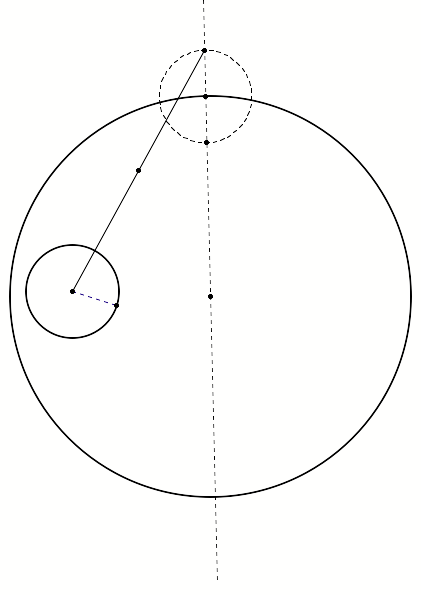
The objective in
connecting those two points and finding the midpoint of the segment is to help
us determine where the center point of the desired tangent circle will be
located. By drawing a perpendicular bisector of this fragment we can determine
the center point for our tangent circle. The point of intersection of the
vertical line through the center and the perpendicular bisector will that
point.
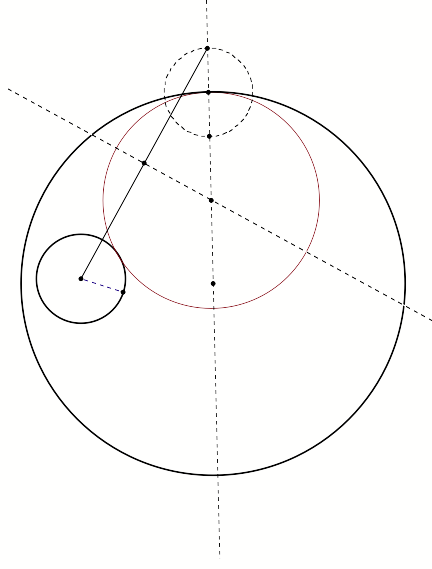
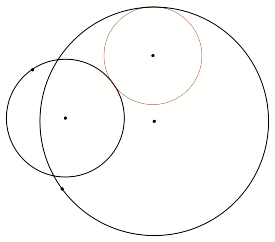
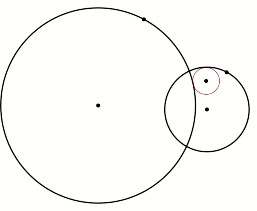
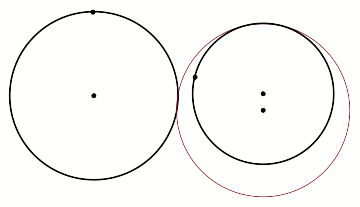
As we can see, the
red circle is tangent to one point on the exterior of the small circle and
tangent to one point on interior of the large circle.
Do not be deceived by
this construction. We can manipulate our figure and the red tangent circle will
still maintain its properties.
Observe the following
maneuvers to see for yourself.
Now lets take a look
at the original construction, and trace the tangent line that intersects the
center point of the tangent circle.
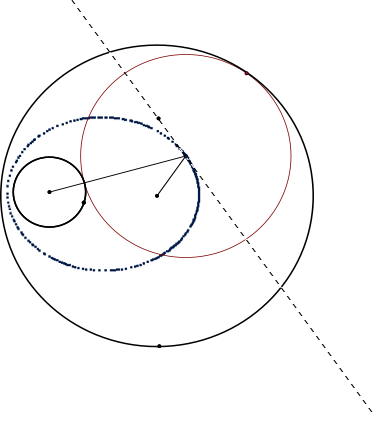
As we can see an ellipse is created in the wake of tracing the tangent line.
What we did here is
to mark the loci of the tangent center point as the tangent point is moved
along the perimeter of the large circle. An ellipse is a collection of points
on a plane where the sum of the distances from any point on the curve to two
fixed points is constant.