
Orthocentric Powers
by
Christa Marie Nathe
In this exploration
we are going to construct several orthocenters of inter-related triangles and
observe some relationships between their orthocenters. In addition we will also construct
circumcircles that are inter-related to both each other and the triangles used
to construct them. Recall that an
orthocenter of a triangle is formed from the intersection of the three lines of
the altitude of the triangle. An altitude is a perpendicular segment from a vertex
to the line of the triangle on the opposite side.
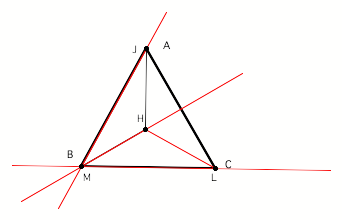
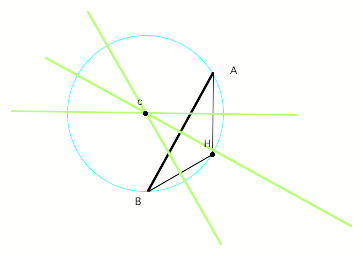
Lets begin with
constructing our basic triangle, which we will label ABC
The orthocenter of
ABC is point H.
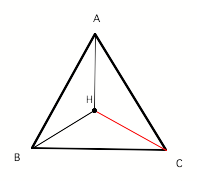
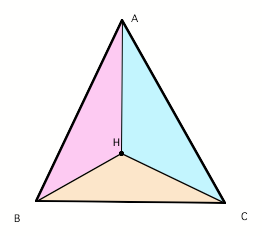
Now we have four
triangles.
ABC
HBC
HAB
HAC
We will now construct
the orthocenters of each of the aforementioned four triangles.
Orthocenter of HBC is
point J, which is also the vertex A of our original triangle.
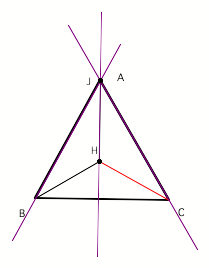
Orthocenter of HAB is
point L and consequently vertex point C of our base ABC triangle.
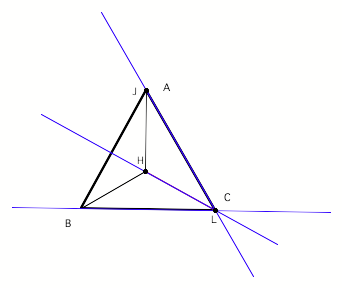
The orthocenter of
HAC is point M, as well as the vertex B of the triangle ABC.
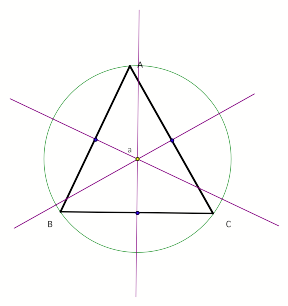
Next we will construct the circumcircles for each triangle
ABC
HBC
HAB
HAC
Remember that circumcircles are constructed via circumcenter point of a triangle. The circumcenter of a triangle is the point that is equidistant from the three vertices of the triangle. By taking the perpendicular bisector of each of the segments between two vertices of the triangle and their intersection it will yield the circumcenter. The circumcircle is the circle created by the vertices of the triangle, with the circumcenter point as its radius.
Circumcircle of ABC
Circumcenter of HBC
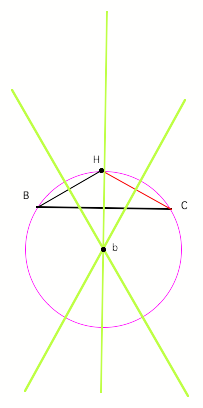
Circumcenter of HAB
Circumcircle of HAC

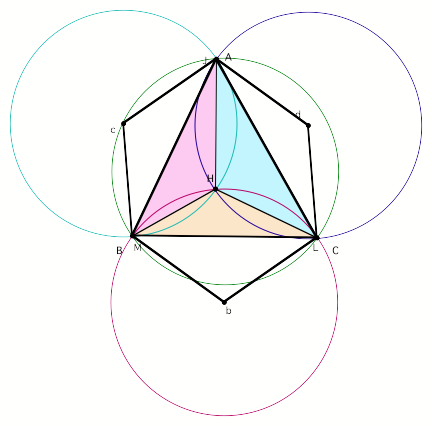
Combining all of our
constructions of the orthocenters for the four triangles, the circumcircles and
connecting the circumcenters we obtain the following figure.
Now that we have made
our composite construction of all of elements, lets see what happens when the
vertex A is moved to where its orthocenter is, that is at point H. As a result,
the pink circle from triangle HBC is swapped with the green circle from ABC
since changing the position of A altered its circumcenter. As H moved, the
triangle HBC became larger thus causing its circumcenter and circumcircle to
shift.
Here,
point H is exchanged with vertex B. Can you anticipate which circle will be
shifted?
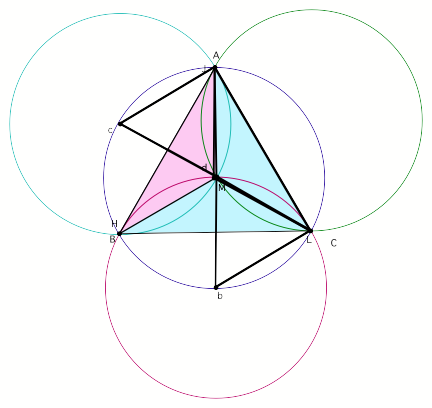
If you expected the
green circumcircle from triangle ABC and the blue circumcircle from triangle
HAC to be swapped then you were correct!
Finally, H is switch
with vertex C and we derive the following construct.
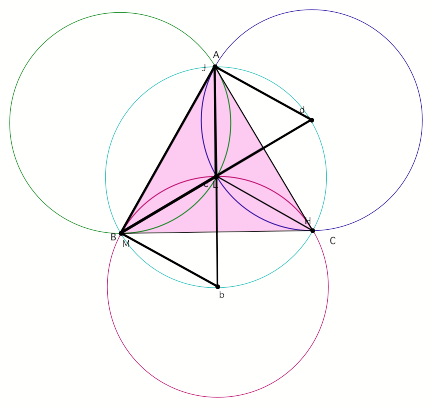
Yes,
the green circle of the ABC triangle and the turquoise circle of the HAB
triangle were switched.