Pedal Point Match
by
Christa Marie Nathe
The construction of a pedal triangle is created with
respect to a pedal point. Take any triangle and label it ABC and pick any point
on the plane that will be the pedal point of the triangle. This point, P, can
either be inside or outside the triangle. Next drop perpendicular lines
from P to the three sides of the
triangle. It may be necessary to extend the lines of the triangle to the extent
that they will intersect the
orthogonal lines dropped from point P.
The points of intersection of the perpendicular lines with the sides (or
extended sides) of the given triangle will form the vertices of the pedal triangle.
Below you can observe some manipulations of triangle
ABC, the pedal triangle with respect to the pedal point P.
In the following investigation we will observe what
happens to the pedal triangle when the pedal point is located at the centroid,
incenter, orthocenter and circumcenter of triangle ABC.
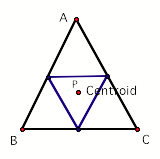
Centroid:
Recall that the centroid of a triangle is created by
the intersection of the three medians, or the intersection of the segment from
a vertex to the midpoint of the opposite side.
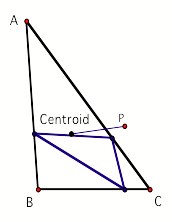
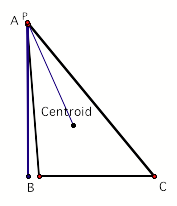
Now letŐs move the pedal point P into a position of
one of the vertices of the triangle to observe what happens to the pedal
triangle. As you can observe, the pedal triangle collapses when P is located at
a vertex.
When the pedal point is matched to the centroid, the
resulting pedal triangle is a medial triangle.
Incenter:
The creation of the incenter of a triangle is a point
in the interior that is equidistant from the three sides. The incenter point
lies on the angle bisector of each angle of the triangle.
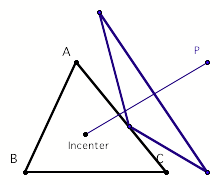
When the pedal point P is matched with the position of
the incenter the pedal triangle becomes the medial triangle.
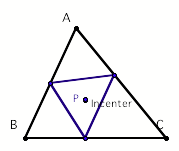
When
Orthocenter:
Constructing the orthocenter of a triangle is as easy
as finding the intersection of the three lines containing the orthogonal
segment from the vertex to the line of the opposite side of the triangle.
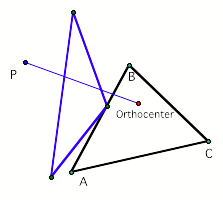
When the pedal point is matched with the orthocenter,
then the pedal triangle will have a perpendicular relationship to the sides of
the ABC triangle.
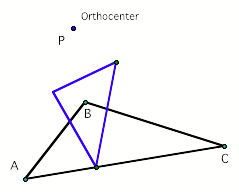
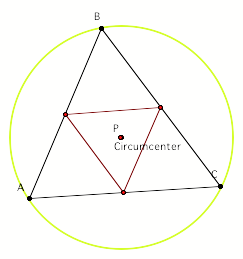
Circumcenter:
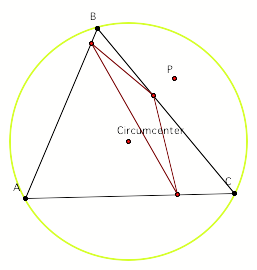
When the pedal point is located anywhere on the
circle, the pedal triangle collapses.
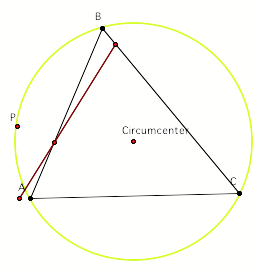
When the pedal point and circumcenter match, it yields
a medial triangle.