
Exploration of some particular conic functions in polar form
Brian Swanagan
We will investigate two similar equations and then a third equation. The first equation and its graph are shown below.
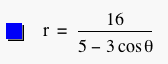
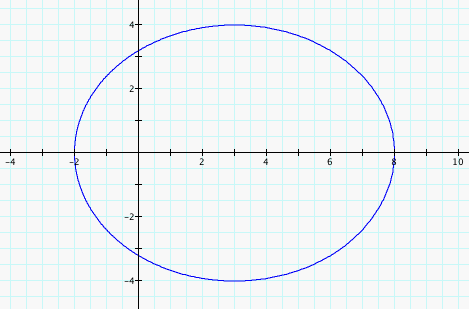
We can see that the graph appears to be an ellipse. The cosine function varies between -1 and 1 so the r value varies between 16/(5-3(-1)) = 2 and 16/(5-3(1)) = 8. When theta is pi/2 or 3*pi/2, r= 16/5. In the graph, it looks like 4 and -4 are the maximum and minimum y-values. Because cosine reaches all values twice between -1 and 1, inclusive, for theta from 0 to 2*pi, it is equal to 3/5 for two theta values. When theta equals these values r = 16/(5 - 3*3/5) = 16/(16/5) = 5. Sin(theta) for these theta values is 4/5 so y = rsin(theta) = 5*4/5 = 4 so 4 and -4 are indeed reached by our equation.
Suppose we make a phase shift by subtracting a value from theta. The graph changes but not dramatically. For example, if we subtract pi/4, we have the following equation and graph.
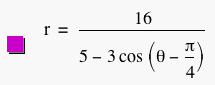
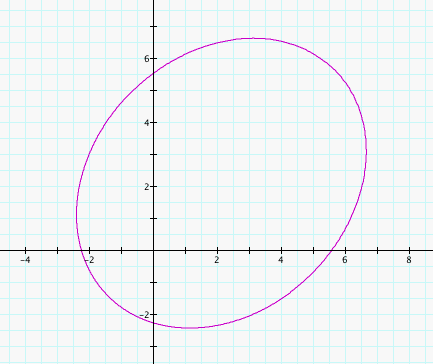
It looks like an ellipse just like the graph of the previous equation. Let T = theta - pi/4. Then, our equation is r = 16/(5 - 3cos(T)) which is exactly our previous equation if T is our angle. But, the angle is theta and theta = T + pi/4 so our r values are reached pi/4 later than before. This causes our original graph to rotate pi/4 radians around the origin. In fact, we can see that is the case if we graph them together simultaneously as below.
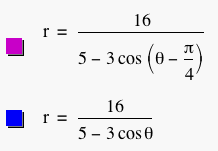
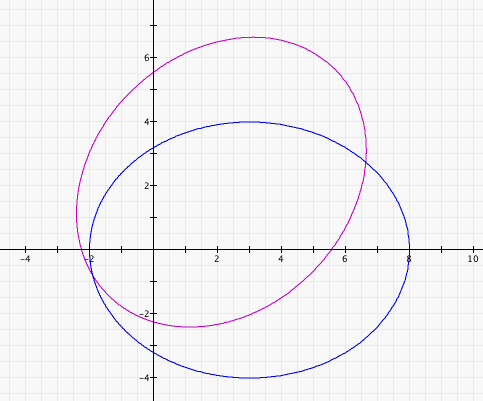
Because we are able to rotate the graph around the origin, I suspect that the origin is a focal point due to the fact that all the wider axes pass through it in this example. If that is true, then (0, 6) would be the other focal point for the blue graph and (6*2^.5/2, 6*2^.5/2) = (3*2^.5, 3*2^.5) for the second (purple) graph. And in fact, if 4 is indeed half the length of our minor axis then the sum of the distances of the foci to either point on the graph at the end of the minor axis is 10 because they form a 3, 4, 5 triangle. We would expect then that the sum of the distances from the foci to the points on the graph that are at the ends of the major axis to be 10 as well. For either case, one foci is 2 away from such a point and the other is 8 away because the distance between them is 6 so the sum of the distances is 10 as we would expect.
This reinforces the possibility that the equations are ellipses. In fact if the foci are indeed the origin and (6, 0) for the blue graph, we would have the following cartesian equation for our ellipse:
(x^2 + y^2)^.5 + ((x-6)^2 + y^2)^.5 = 10
Let T be theta and x = rcosT and y = rsinT so that we convert the equation into polar form.
((rcosT)^2 + (rsinT)^2)^.5 + ((rcosT - 6)^2 + (rsinT)^2)^.5 = 10
r + ( r^2 - 12rcosT + 36)^.5 = 10
r^2 - 12rcosT + 36 = (10 - r)^2 = 100 - 20r + r^2
20r - 12rcosT = 64
r(20 - 12cosT) = 64
r = 64/(20 - 12cosT) = 16/(5 - 3cosT)
Aha! So, our first polar equation is an ellipse afterall as is our second because it is simply a rotation around the origin pi/4 radians.
Now, let's explore another quite different equation.
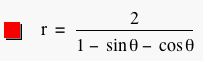
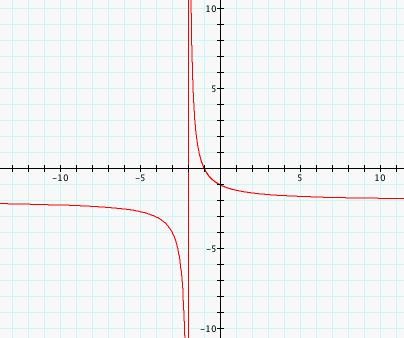
The graph appears to be hyperbolic. We can see that the asymptotes to the graph appear to be at x= -2 and y=-2. The asymptotes would occur when 1 - sin(theta) - cos(theta) = 0. So, sin(theta) + cos(theta) = 1 and sin(theta)^2 + 2sin(theta)cos(theta) + cos(theta)^2 = 1 if we square both sides. Then, we have sin(2theta) = 0 which implies that theta is either 0 or pi/2. When theta is 0, sin(theta) is 0 and cos(theta) is 1 so 1 - 0 - 1 gives us 0. When theta is pi/2, sin(theta) is 1 and cos(theta) is 0 so 1 - 1 - 0 gives us 0 as well.
y = rsinT where T is theta so assuming sinT is not 0, we have
y = rsinT = 2/(1 - sinT - cosT)*sinT = 2/(1-sinT - cosT)*(1+sinT+cosT)/(1+sinT+cosT)*sinT = 2(1+sinT+cosT)/(-2sinTcosT)*sinT = -(1+sinT+cosT)/cosT
so when T approaches 0, y approaches -(1+0+1)/1 = -2.
Similarly, x = rcosT = -(1+sinT+cosT)/sinT when cosT is not 0 so as T approaches pi/2, x approaches -(1+1+0)/1 = -2 as well.
Thus, x = -2 and y = -2 are assymptotes for our functions after all. Again if we created a phase shift by adding to our theta value inside the function, the function would rotate around the origin. For this reason, I suspect the origin again to be a focus for our graph which would make (-4, -4) the other focus simply because the graph has a line of symmetry at y = -x -4 and y=x which we could guess because the asymptotes are symmetrical about the line y = -x - 4 and and y = x. The points (-1, 0) and (0, -1) lie on the graphs at pi and 3pi/2, respectively, so the difference of the distances of these two points to the foci is 4.
The cartesian equation for such a hyperbola would be
((x+4)^2 + (y+4)^2)^.5 - (x^2 + y^2) = 4.
Converting to polar, we have
((rcosT + 4)^2 + (rsinT + 4)^2)^.5 - ((rcosT)^2 + (rsinT)^2) = 4
(r^2 + 8r(sinT + cosT) + 32)^.5 - r = 4
r^2 + 8r(sinT + cosT) + 32 = 16 + 8r + r^2
-8r(1 - sinT - cosT) = -16
r = 2/(1 - sinT - cosT).
Aha! Indeed, our polar equation is a hyperbolic function after all!