Sequences Similar to Fibonnaci

Brian Swanagan

 

The sequences we will look at will be of the form a_(n+1) = a_n + a_(n-1) where a_0 and a_1 vary.

 

First, let's take a look at the Fibonnaci sequence. a_0 = 1 and a_1 = 1. The first column gives each consecutive term where the nth row is the a_(n-1) term. The second column gives the a_(n-2) term and the third column gives a_(n-1)/a_(n-2).

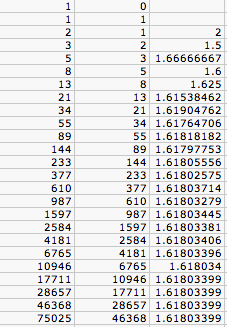
We can see that the ratio of consecutive terms approaches a limit quickly and is approximately 1.61803399.

 

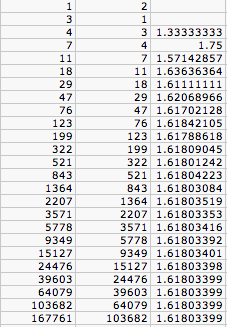
Now, let's look at the Lucas sequence where a_0=1 and 1_1=3. We see that it approaches a limit apparently even faster than the Fibonnaci sequence and appears to be the same limit.

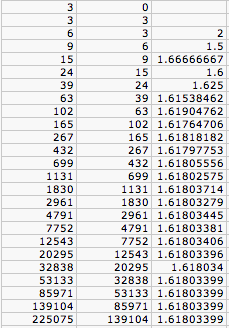
What if we multiply the Fibonnaci's starting numbers by a number, say 3. Then a_0 = 3 and a_1 = 3. The terms appear to all to be 3 times the terms of the Fibonnaci sequence. That makes sense because a_(n+1) = a_n + a_(n-1) = 3F_n + 3F_(n-1) = 3F_(n+1) where F_n is the nth Fibonnaci number. a_n/a_(n-1) = 3F_n/3F_(n-1) = F_n/F_(n-1) so the ratio should still approach the same value as we can see it does in the spreadsheet below.

We have tried when a_0 = a_1 and when a_0 < a_1. Let's try a_0 > a_1. Let a_0 = 5 and a_1 = 1.

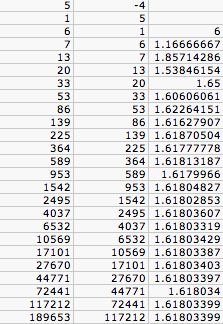
The ratios still appear to approach the same value as before although at possibly a slower pace.

 

Why does the limit remain the same for the sequences we have seen and is it the same for all such sequences of the form a_(n+1) = a_n + a_(n-1).

Suppose the limit of a_(n+1)/a_n approaches x as n approaches infinity. Let X equal this limit.

 

Then X^2 = lim[ a_(n+1)/a_n * a_n / a_(n-1) ] = lim[ a_(n+1)/a_(n-1) ] = lim[ ( a_n + a_(n-1) )/a_(n-1) ] = lim[ a_n/a_(n-1) + 1] = X + 1.

 

So, X^2 = X + 1. Then, X^2 - X - 1 = 0. The quadratic equation gives us that X = [1 +/- 5^.5]/2. In the case where a_(n+1) and a_n are both positive or negative then the limit is positive so X=(1+5^.5)/2.

Furthermore, (1+5^.5)/2 is approximately 1.61803399 so our sequences appear to approach it after all.