Let's examine the xy-term of the equation x^2 + axy + y^2 = 9. When a=0, we can easily see that the equation becomes one for a circle but what happens for a variety of a values. I first tried 0, 1, 2, 3, and 4 for my a-values to see what type of graphs I would get.

 

 

 

I then tried negative values to see if I would get similar graphs.

 

 

These turn out to simply be a reflection over the y-axis. To get a better view of this to make sure they are essentially reflections, I graphed the first set in red and the second in blue and the shared circle graph in purple.

In the purple, we have a circle graph. The first blue and red graphs give us an ellipse. The second blue and red graphs give lines. The last blue and red graphs give us hyperbolas.

 

a=0 and 2 or -2 appear to be our boundaries. From the pictures of the graphs alone, we can hypothesize that a=0 gives us our only circle, that a=2 or -2 give us our only lines, that between 0 and 2 or between 0 and -2 we get ellipses, and that a greater than 2 or a less than -2 give us hyperbolas. How do we know for sure that this is the case?

 

We might try manipulating the equation x^2 + axy + y^2 = 9.

x^2 + axy + y^2 = 9

x^2 + a^2/4*x^2+ axy+ y^2 = 9 + a^2/4*x^2

(a/2*x+y)^2 = 9 + (a^2/4-1)x^2

a/2x + y = +/-(9 + (a^2/4-1)x^2)^.5

y = +/-(9 + (a^2/4 - 1)x^2)^.5 -a/2*x

When a= 0, the a/2*x term becomes 0 and we are left with the distance formula in terms of the distance, 3, and the x-coordinate so we have a circle circled in this case around (0,0).

When a=2 or -2, the (a^2/4 - 1) term becomes 0. Then we have y = +/-3 -a/2*x which gives us two lines for each a-value 2 and -2.

Now when 2>a>0 or 0>a>0, (a^2/4 - 1) remains negative giving us a distorted version of the distance formula which results in these cases result in ellipses because if we go alter the equation in order to move the x^2 term back to the same side as the y^2 they have the same sign value.

For a>2 or -2>a, (a^2/4 - 1) has a positive value which changes which gives us different signs for y^2 and x^2 if put on the same side of the equation which gives us hyperbolas.

No other a-values give us critical changes in the graph where either signs change or terms disappear (0, -2, 2).

 

Another interesting investigation might be to see what happens to the graphs as they approach (0, -2, 2).

 

First, we will see what happens as a approaches 0 from the positive side. I started with a=1 (red) and multiplied it by 1/4 (blue) and then 1/4 again (green) and finally graphed when a=0 (purple).

 

Then, I graphed the same thing but for negative values of a. We can see that the graph becomes more circular as a approaches 0 fairly quickly.

 

Afterwards, I looked at the graphs as they approached 2 and -2 from the negative and positive sides respectively.

The a-values above I used were 1 (red), 1.75 (blue), 1.9375 (green), 2 (purple) and the negative of the same values in the graph below. We can see that in both cases the graphs begin as ellipses that become much more stretched out to more closely match the 2 line graphs which might be moved as an infinitely stretched ellipse. Notice that I zoomed out from the view compared to the others because the ellipses were quite stretched out in fact which makes for the distortion in the thickness of the graphs.

 

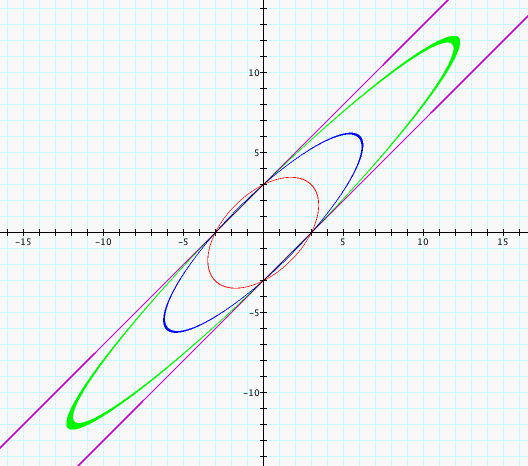
Now, we explore what happens to the graphs as the a-value approaches 2 and -2 from the positive and negative directions, respectively.

 

Above, I used the values 3 (red), 2.25 (blue), and 2.0625 (green). We can see that we have hyperbolas that appear to stretch out more along the lines y= -3x+3 and y= -3x-3. Below, we simply have the corresponding negative values and the lines y= 3x+3 and y= 3x-3.

Finally, we investigate what occurs when we increase the magnitude of our a-values greatly.

 

In the graph above, we have a-values of 2 (purple), 20 (red), 200 (blue), and 2000 (green). The graphs begin to approach the axes as the magnitude of our a-value increases greatly. Below, the graph is the same but only zoomed out a bit.

 

In conclusion from our equation x^2 + axy + y^2 = 9, we can create circles, ellipses, lines, and hyperbolas. When a=0, we have a circle. For values of a between 0 and 2 or 0 and -2, the graph is an ellipse. The graph becomes 2 lines for a= 2 or a= -2. When the magnitude of a is greater than 2, then we have hyperbolas. As our a-values approach 0 (circle), 2(lines), or infinity (axes), we have graphs that approach the appropriate graphs.