2x+b=0 in relation to ax^2+bx+c=0 in the bx plane

Brian Swanagan

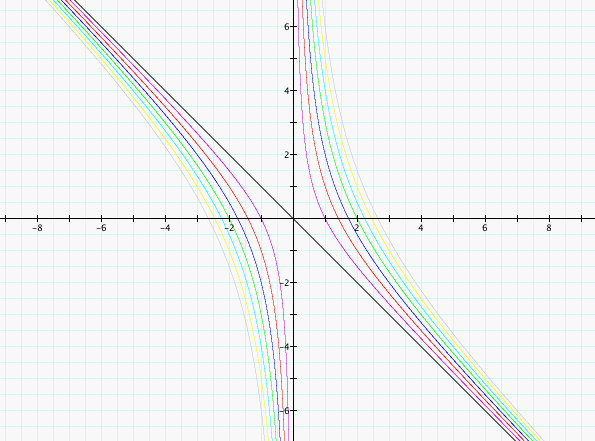
During this exploration, we observe some quadratic graphs in the xb-plane. Initially, we will vary the c-values while keeping them positive as shown below in the next graph.

 

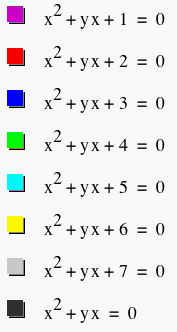
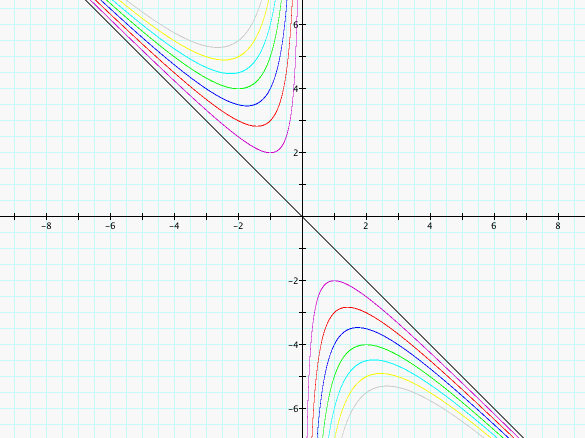
The result is a set of hyperbolas that approach the lines y = -x and x = 0.

Now, let's add the graph 2x+b=0 to our graphs in the xb-plane.

 

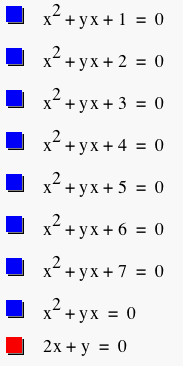
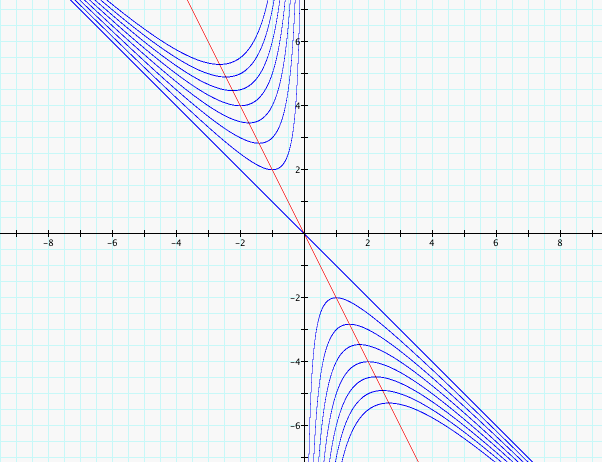
We see that the 2x + y = 0 passes through the minimum and maximum values of the higher and lower parts of the graph, respectively and that it intersects with the two lines at the same point.

Next, we look at negative values of c.

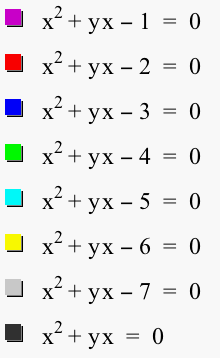
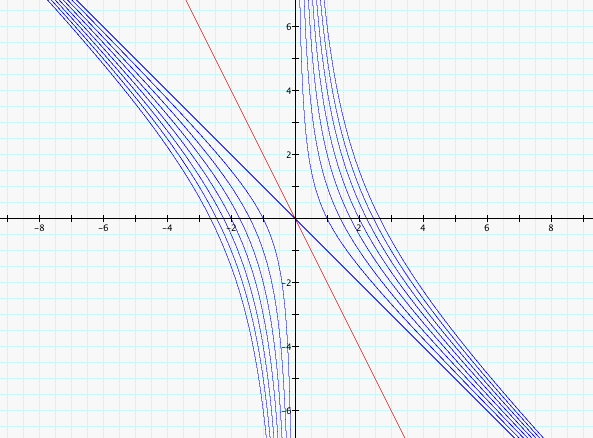
This time the hyberbolas approach the lines from the two other portions and cross the x-axis without having a minimum or maximum value.

Let's add our 2x+b=0 graph again.

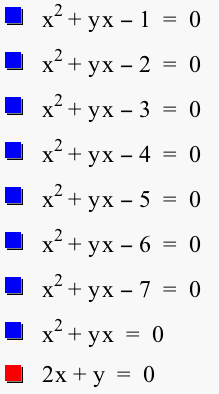
Finally, let's take a look at what happens when our a-value is negative. Here, we have our c=0 (purple), positive c-values (blue), and negative c-values (green).

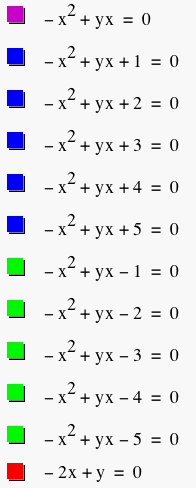
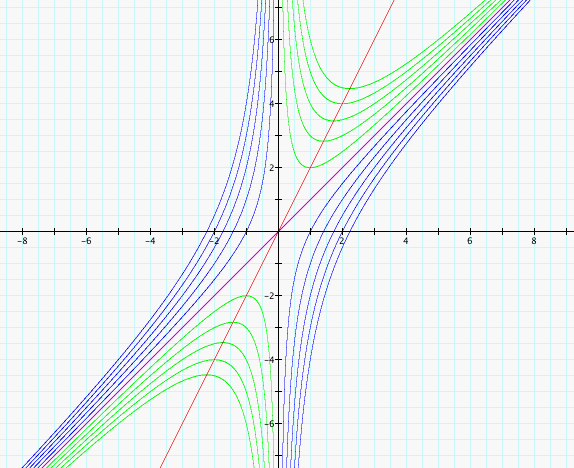
Again, the red graph hits the minimum and maximum values of the higher and lower portions of the green graphs, respectively and seem to be a mirror for the two halves of the blue graphs.

The quadratic formula gives x-values where the graphs are 0: x = [ -b +/- (b^2 - 4ac)^.5]/[2a]. The arithmetic mean for these x-values is -b/(2a) which corresponds to our red graph. When we have a=1, we graphed x = -b/2 and when a=-1, we graphed x = b/2. We see that when a/c > 0 from the above graphs, that we have a point that intersects the red graph. This is where b^2 - 4ac = 0. When, a/c < 0, then -4ac > 0 and b^2 - 4ac > 0 despite the value of b so they never intersect our red graph. These equations always have two solutions for each b-value.