Equal Segments of an Angle

Brian Swanagan

 

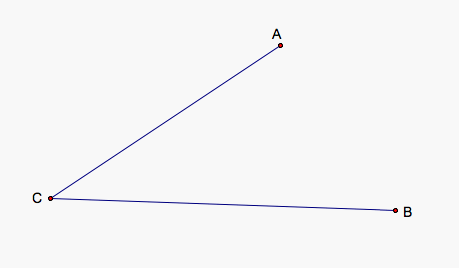
Given 3 different points, A, B, and C, we would like to create a point X on AC and a point Y on CB so that AX = XY = YB. At the moment, we will use the nonlinear set of points shown above where AC and CB are not very different in length. We will discuss how to adjust for other, less generous cases later.

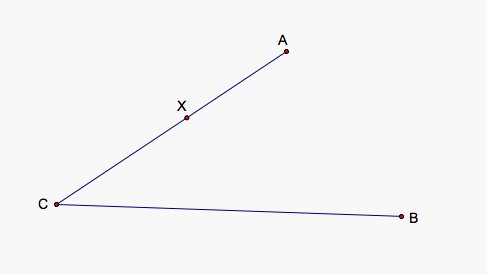
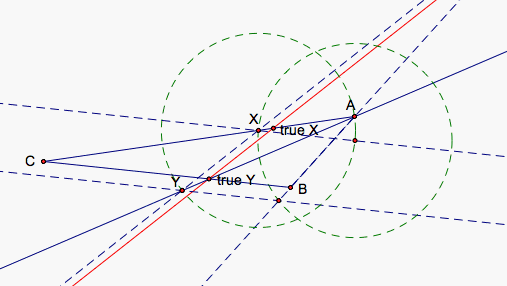
We start of course by creating a point X on the segment AC. If AX = XY, then Y will lie on the circle that contains A and whose center is at X. But, how do we determine Y's location. We want to ensure that Y is equidistant from both X and B so we need to create a rhombus with two sides parallel to CB. That way we can move X along AC until Y touches CB which would give us our point and then the lower side of the rhombus would essentially be YB.

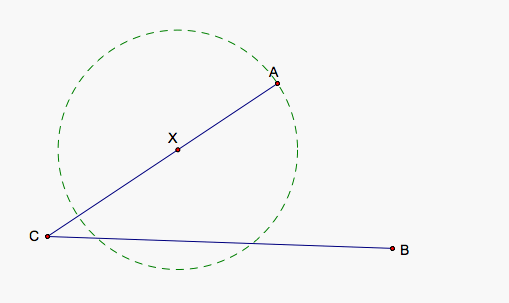
In a rhombus, opposite sides are parallel so we need a to draw a parallel line to CB through X and find the intersection with the circle we drew before to find an adjacent point to X on our rhombus.

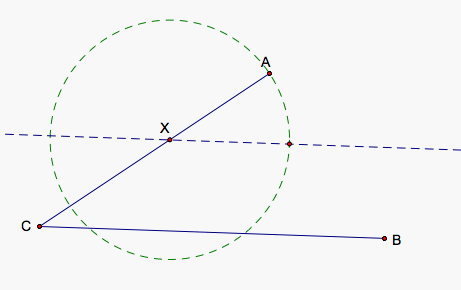
We need another point on our rhombus to define our final locations. We can draw the segment AB and draw a new circle around our recently found point. The circle will intersect with AB unless unless AX is too large or if A = B. But supposing we have three different points as stated initially above, we can make XA close enough so that our second circle intersects AB. And if we instead draw a line rather than a segment through AB, it may be more helpful in other situations as mentioned later.

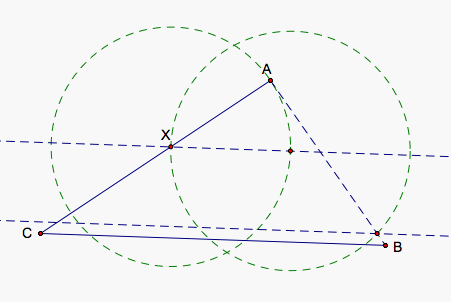
Once we find this third point from the intersection of our second circle and AB, we now can construct a rhombus. We draw a line parallel to CB through our third point and find the intersection with this new line with our first circle. This point we shall label Y.

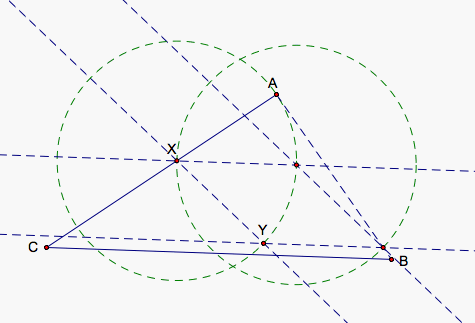
We simply move X along AC until Y lies close to BC and we can get a good idea for Y's actual location on BC.

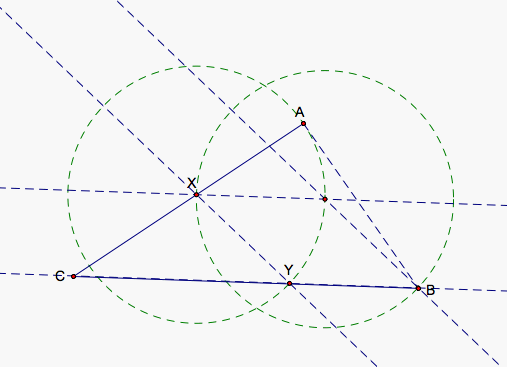
In order to find Y's true location, we can draw a line through A and Y and find its intersection with BC. We can see that as we move X, Y moves along this line creating a series of triangles similar to AXY. We know this because the angle AXY is fixed and AX = XY so we have a series of isosceles triangles with the same fixed angle at X. This means XYA and YAX are equal angles as well telling us that they are also fixed. The intersection of line AY and segment BC gives us our point (true Y) that Y approaches as the line through Y parallel to BC approaches BC as we change our X appropriately.

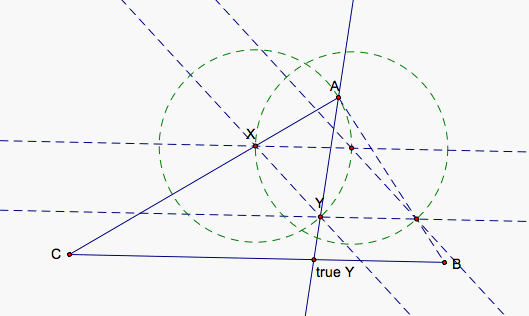
Now, we draw a final line (red) through the point (true Y) and parallel to the line through XY. The intersection of this red line with AC gives us our (true X) point. As we move X closer to (true X), y moves closer to (true Y) because the triangles A(true X)(true Y) and AXY are similar triangles.

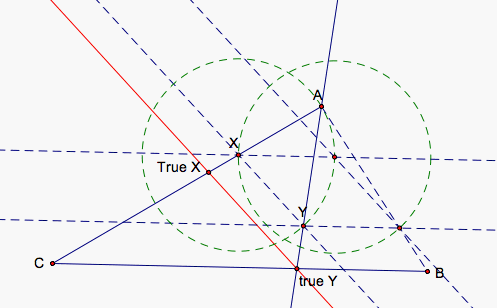
After hiding our construction circles, lines, points, and segments and after renaming (true X) as X and (true Y) as Y, we now have what we wanted: a line through AC and BC that intersects AC at X and BC at Y where AX = XY = YB.

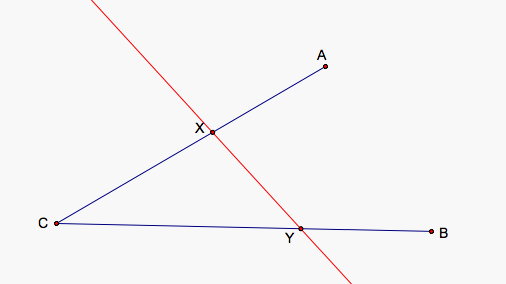
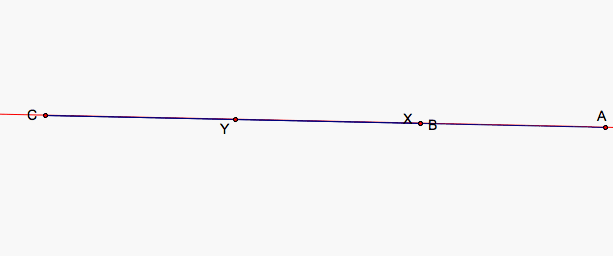
We run into problems with our construction if CB is less than half the length of AC, AC is less than half the length of BC, and if A, C, and B are colinear. If the points are colinear, then X = B so AX = AY/2 = AB = BY = XY which gives us AX = XY = YB. In the two other instances, we could instead create lines through AC and BC and find points along the lines rather than the segments so that AX = XY = YB where X lies on line through AC and Y on the line through BC. We may not, however, be interested in such cases.

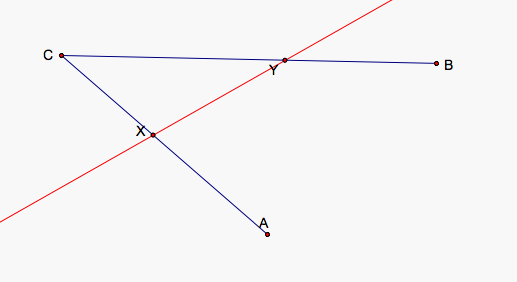
The construction holds if the orientation of ACB is flipped as well.

And finally, a case mentioned earlier may require another adjustment. A and B may be quite close together if ACB is a small angle so that the circle around X does not intersect AB except for small values of lengths for XA which may not be desireable. We can instead draw a line through AB rather than a segment to help this situation. Then the circle around X will intersect line AB at some point unless A = B but A and B are different points.

In the picture above, we show a case when we might be interested in drawing a line through AB rather than a segment. We can see, however, that we could have move X closer to A and still generated our desired rhombus. Yet, it might be difficult to do so if A and B are extremely close so using the line instead would allow for an easier construction of a larger rhombus while not actually necessary. Below, we have hidden our constructions. The problem here is not in the concept of construction the rhombus itself but in possible difficulties because of whatever tools you might be using or with human eyesight.

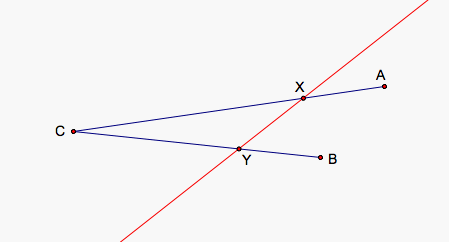
Creating a rhombus, gives us our desired result and only has a few issues with certain instances. When CB < 2AC, AC < 2CB, or they are colinear points, we cannot find points X and Y along the segment AC and CB, respectively, such that AX = XY = YB.