Simson lines along sides of a triangle

Brian Swanagan

 

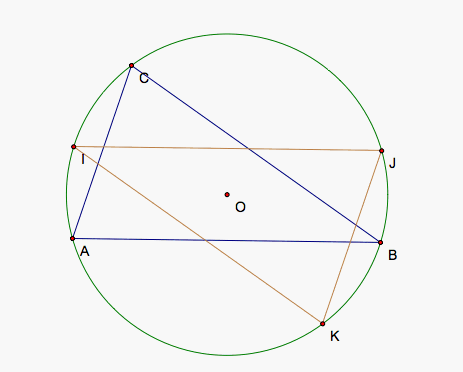
We would like to see if there is a simpson line that lies along any side of our triangle. First, we have constructed a triangle ABC as an example to illustrate the steps we will take to determine whether or not we can find a location for our pedal point so that the line lies along a side of our triangle. Most importantly, we should note that from prior investigations that we determined that simpson lines exist and only exist when the pedal point lies on the circumcircle of ABC. For that reason, we have constructed our circumcenter and circumcircle.

 

Let's begin with side AC. We need all three points of our pedal triangle to lie on the line through AC. Each point of our pedal triangle lies on a different line through each of our sides. In order for all of them to lie on the side AC, then the point that lies on the line through AB must be located at A because that is the only point where the lines through AC and AB intersect. Similarly, the point that lies on BC must be located at C. The third point already exists on AC. If we draw perpendicular lines to AB and BC through A and B respectively, then I lies at their intersection. If I lies on the circumcircle of ABC, then we know such a point exists such that our simpson line lies along AC.

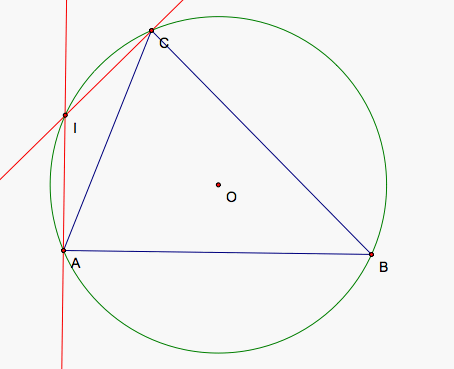
The construction itself gives us the location for the pedal point, I, such that we have the desired simpson line along AC. The only problem in the construction would be if the perpendicular lines did not cross or in other words are parallel. If the perpendicular lines to the two sides AB and BC are parallel, then AB and BC are parallel, a contradiction because then B is a straight angle so that we do not have a triangle but instead three concurrent parallel lines through each pair of three points.

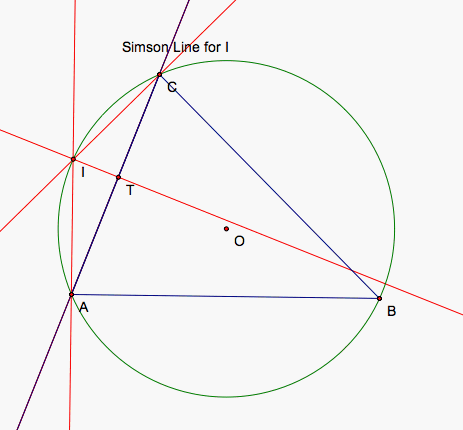
Now we know we can find the location of our pedal point I so that the line AI is perpendicular to AB and the line CI is perpendicular to BC and the third necessary point, T, we can find by drawing a perpendicular line to AC through I. Connecting these three points gives us the colinear points of our simpson line that would define our pedal triangle if I did not lie on the circumcircle.

For the simpson line along BC, we draw perpendicular lines to AB and CA through B and C respectively and find their intersection, J, which will be the location for the desired pedal point. For side CA, we draw perpendicular lines to AB and CA through A and C respectively to find our pedal point, K.

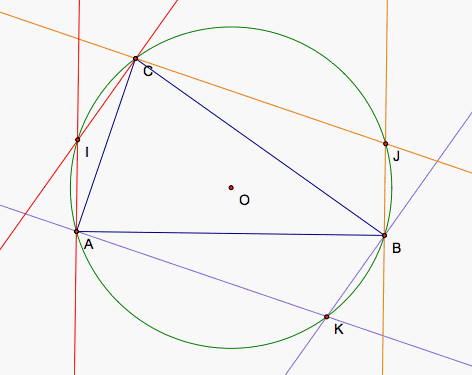
Another interesting exploration would be to look at the triangle JIK formed by our three pedal points and how it relates to our original triangle.

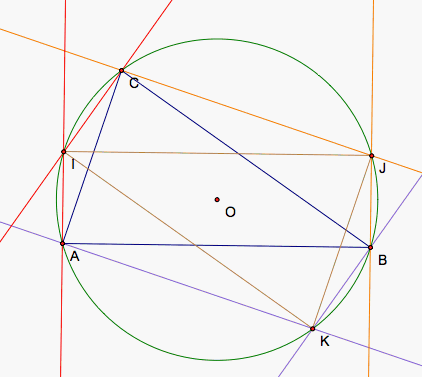
As we constructed our first pedal point I, we used the perpendicular line of AB through A which now we can denote as IA. Because IA is perpendicular to AB, the angle IAB is a right angle and A lies on the circumcircle so IB is a diameter of the circumcircle. We can see that it passes through circumcenter O just as we would expect of a diameter for a circle. That means I is simply a 180 degree rotation of B around O.

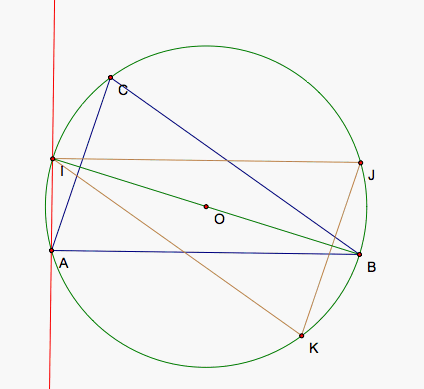
Similarly, JAC is a right angle because JC is perpendicular to CA. Then, JA is a diameter of the circumcenter so J is a 180 degree rotation of A around O.

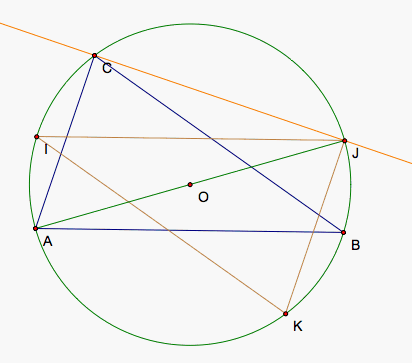
Lastly, KBC is a right angle because KB is perpendicular to BC so KC is a diameter of the circumcircle. Then, K is a 180 degree rotation of C around O. That means triangle JIK is a 180 degree rotation of triangle ABC around O so JIK and ABC are congruent triangles.

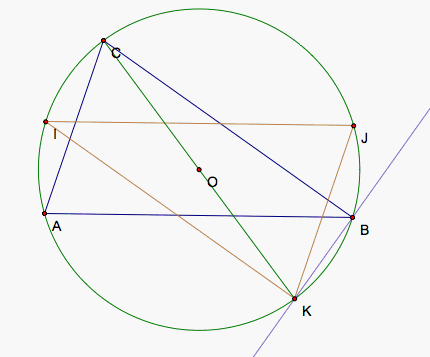
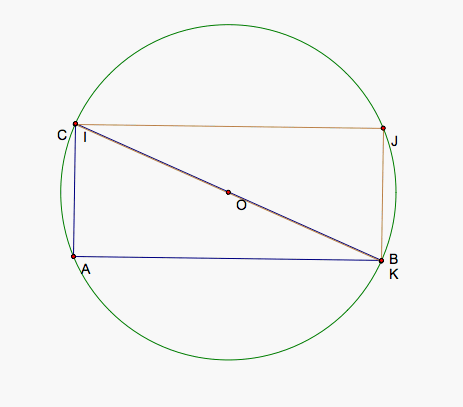
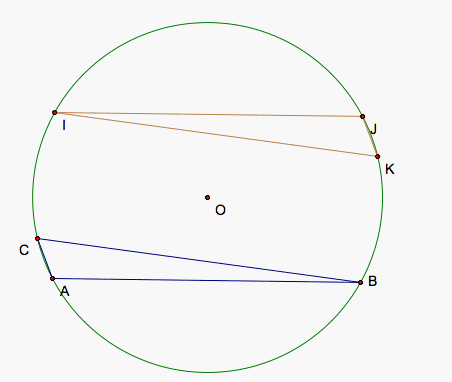
Below, we can see some examples of triangles, their circumcircles, and the triangle made up of 3 pedal points whose simpson lines exist along the sides of the triangles. The first is the triangle we worked with above, an accute triangle. The second is a right triangle so that we can see that BC and IK are already diameters of the circumcircle. The third triangle is an obtuse triangle so that we can see the pedal point triangle and the original triangle do not necessarily touch.