Brian Gleason and I, Brian Swanagan, have explored a matter of interest concerning minimal polynomials in Q[x], the set polynomials with rational coefficients, of sums of two values whose minimal polynomials are easy to determine and of which whose roots are also not particularly difficult to find. There are some steps in our process that we have had trouble proving or looking at in depth but I have come up with some miniature questions related to our quandaries. One of which is whether f(x-(a+bi))*f(x+(a+bi)) is an element of Q[x] when f(x) is. We can break this down a bit. If we can prove that f(x-a)*f(x+a) is and f(x-bi)*f(x+bi) is, then we can prove by applying one and then the other that the former polynomial is also in Q[x]. Still, this is a bit complicated so I have decided to explore particular f(x) of the form x^n.

Clearly, x^n is an element of Q[x].

Then, I would like to know if (x-bi)^n(x+bi)^n is also.

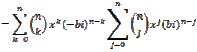
Now, we must consider some cases. When m is odd, we have an even number of terms in the sum and they are symmetric in that the first half of the terms are the same as the second half but only with a sign change so that the entire sum becomes zero.

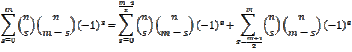
due to the following:

because m is odd.

When m is even, then 2n-m is even so that (bi)^(2n-m) is b^(2n-m)i^(2n-m) = +/- b^(2n-m) so as long as long as b^(even) is in Q then (x+bi)^n*(x-bi)^n is an element of Q[x].