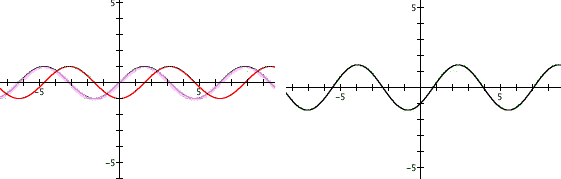Sine (or sinusoid) waves are functions that we often see in Mathematics, Physics, Electrical Engineering and other fields of science. In this exploration, we will look at the sinusodial wave
and the different values of a, b, and c.
First, let's look at
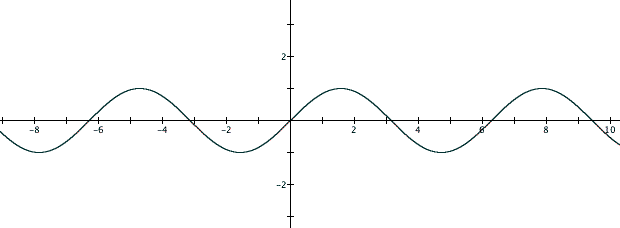
Since a (which is also known as the amplitude) is an understood 1, then this is always the max and minimum point of the graph. We also see that it is symmetric with respect to the origin of the cartesian plane which lets us know that the graph is an odd function. After rotating 180 degrees about the origin, the graph still is unchanged. If we look at a graph when a is greater than 1, we get the following graph:
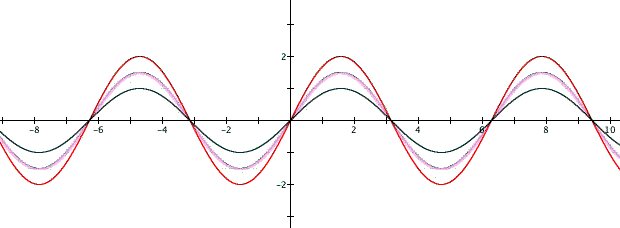
Here our graphs are:
So, we can see that the value of a elongates the wave vertically. Since a is the amplitude it will determine the maximum and minimum points of the graph.
if we explore waves with various values of b and c, we get the following:
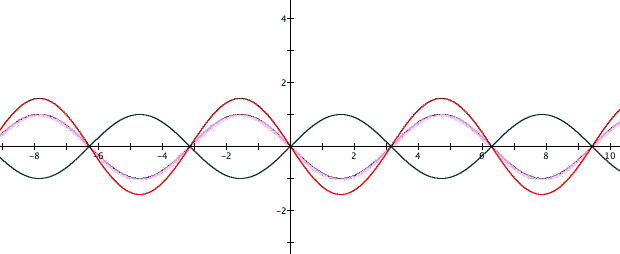
Here our graphs are:
The pattern that we see is that if a is negative then it changes the wave's magnitude of oscillation. We can see that the intercepts remain the same regardless if a is negative or positive.
All of these different graphs are what is known as a periodic motion. It is often called simple harmonic motion. Now we explore what will happen if the constant b varies in the graph.
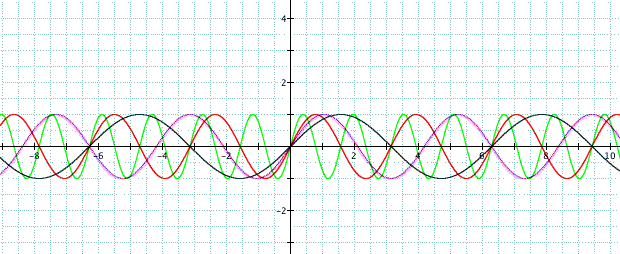
Unlike the value of a, it looks like the value of b compresses the graph closer around the x-axis. Look HERE to see what happens as b changes from negative to positive.
So we know that different values of a changes the graph vertically and different values of b changes the graph horizontally, now lets see what happens when we add the constant c to our graph.
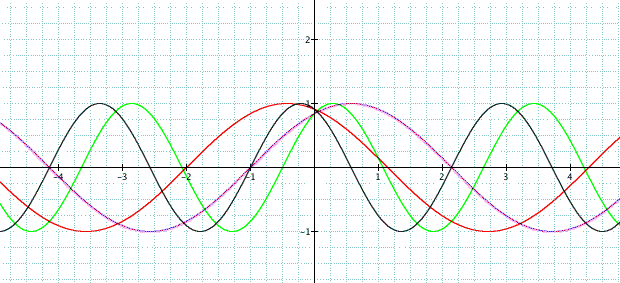
Here our graphs are:
Well, if we look at the first two graphs in purple and red, we can see that there is a vertical shift. Likewise, if we look at the last two graphs, there is a vertical shift of one unit. The values of b and c affect the phase shift displacement of the graph. And we can clearly see that it is a shift in a horizontal direction from its normal position.
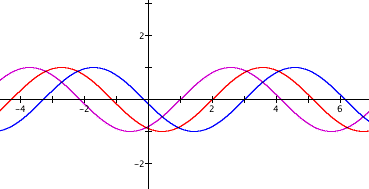
Here our graphs are:
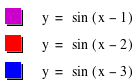
So our graphs show a vertical shift to the right which leads us to the conclusion that if the phase shift is positive, it shifts to the right and if it is negative, it shifts to the left.
ANOTHER EXPLORATION: What would happen if we take two sine graphs with the same amplitude but a different frequency and add them together?
Suppose we had the following graphs:
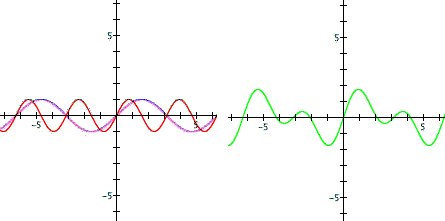
The graph on the left are two separate sine wave with the same amplitude, however if we look at the graph on the right it is the sum of the two waves. This creates a phenomenon called "beating" waves. We can see that the amplitude actually increases when they are added together. This kind of exploration leads into what is known as a fourier series or theorem which is the sum of sine waves. Look at the following graphs and see what kind of conclusions we can figure out about the value of c:
y = sin x (PURPLE)
![]() (RED)
(RED)
INTERESTING???
y = sin x (PURPLE)
![]() (RED)
(RED)