In this explorations we want to look at parametric curves but first let's look at the rational form of a circle.
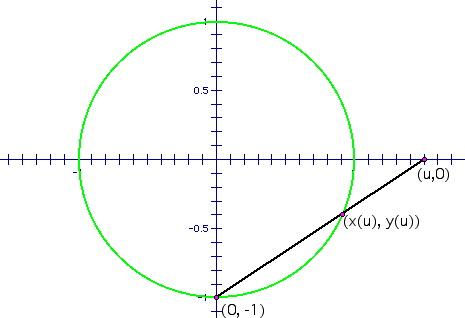
So we see that
this is a circle with a radius 1 where u represents out parameter
(imagine the scale isn't there). So u is the value of the x-axis and for
any value of u we will have a point
(u,0). Obviously, we
can see that the line that joins the point (0,-1) and (u,0) intersects the
circle at two points (let the other point be (x,(u), y(u)). Therefore, we derive the following
equation: x = uy + u and we know that the circle equation is 
, so using the circle equation we can plug
our line equation. When we solve it for y, the results are two roots where one
is -1 and the other is 
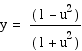. When we plug this
into our line equation we get 
, therefore
we get the following equations for each u: 
and
. From this we know that the trigonometric
parametric form is the following (where t ranges from 0 to 2PI)
and 
Now let's explore some basic equations first.
We will start
off with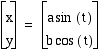 
We see that we actually get the unit circle. what if we change the values of a and b.
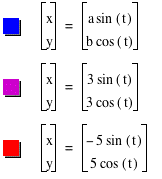
We see that our results are just simple. a is the positive and negative value on the x-axis while b is the positive and negative value on the y-axis. What if we have different values for a and b? What kind of shape would we get? Ellipse maybe?
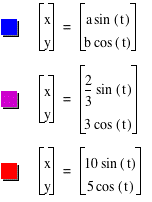
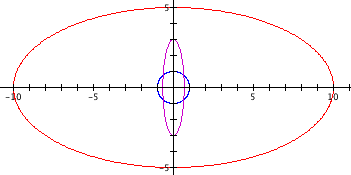
Yep, it is
an ellipse. We know that an ellipse formula is 
for
some a
and b. How did we get our
parametric equation from that ellipse formula? Remember in order
to derive our parametric form, we replaced y with b sin(t) and solved for x.
Now, that we
can clearly see when our vector z= 0 and a and b are equal, we get
a circle and when a and b vary from each other then we get an
ellipse. So an extension to this exploration could be...what would
happen if we let z equal something, say
where t ranges from 0 to 6pi?
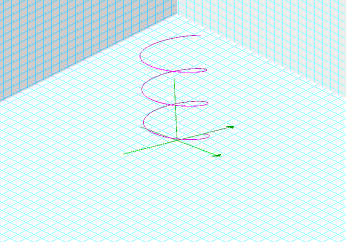
OK...this is
neat!!! And since we know that 
= 
, the curve must lie on the circular cylinder
. As t increases from 0 to 6pi,
the point (x, y, z) moves in an upward clockwise cylinder creating
a circular curve that is called a helix.
What about this parametric equation:
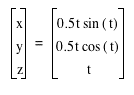
Look HERE to see the graph. We have another circular curve. what does it resemble? A tornado possibly!!
from that graph
we know that if we eliminate our t parameter, this curve will
lie on the cone 
.
How about this parametric equation:
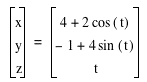
Look HERE to see graph! This curve lies on what?