In this exploration, we want to look various graphs that have a different value of a if given the following function:
These graphs tend to be symmetric around the y-axis. So lets start our by looking at
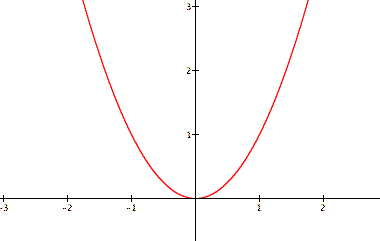
Ok..we have a parabola that is concave upward. We can see that the graph is also symmetric with respect to the y-axis and its vertex is the point (0,0). Now lets look at graphs where a is greater than 1.
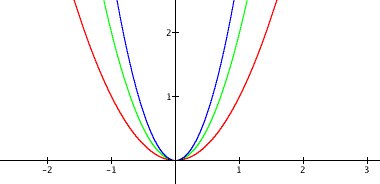
Clearly, here we can see that the parabola is stretching vertically and as when a increases each of the points on the parabola rises away quickly from the vertex. When can also see that when a is positive, the graph is concave upward. Each parabola in this form share the same vertex point. Let's look at a graph with a that is less than 1.
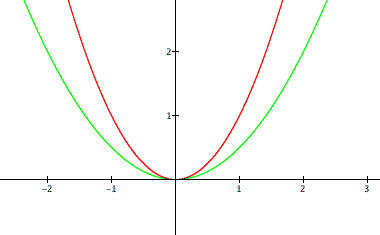
We find that this graph is expanding and each of the points rise away slowly from the vertex.
The smaller a gets, the closer the graph gets to the x-axis. Look at the following graphs.
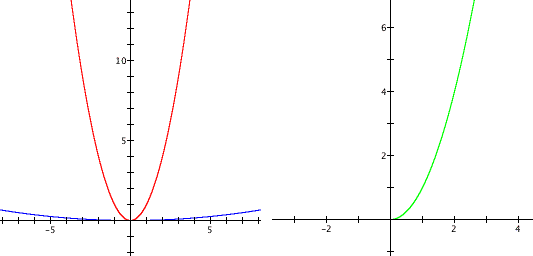
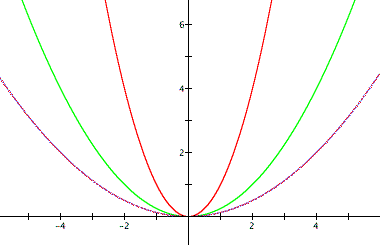
If look at the graphs on the
left, we can clearly see as a approaches zero, the closer the parabola
gets to the x-axis. Now, if we look at the graph
on the right, we can see that it looks more like an expontential
function that lies in the first quadrant. Why is this? If we simplify
that function, don't we get 
. Well,
remember that negative numbers under the radical are imaginery
numbers therefore this particular function has bound. The square
root of x is the inverse function of x square.
Now, let's explore graphs when a is negative.
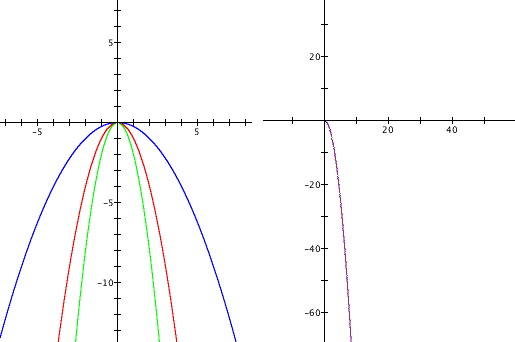
Here we can see that the parabolas on the left are concave downward and are symmetric to the y-axis. In addition, as a approaches negative infinity the graphs compress vertically and becomes narrow. The graph on the right (in purple) looks like a reflection of the other above it. So it seems like a plays a vital role in the dimensions of the parabola. Look HERE to see what happens as a increases and decreases.
From this exploration, we know that the focus is (0,1/4a) and the directrix is -1/4a
What if we add a constant to our graph? What kind of changes should we expect? Lets explore graphs with the constant d added and subtracted.
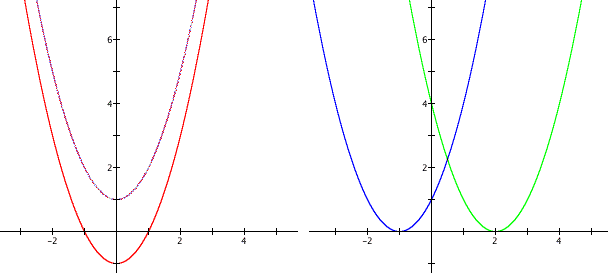
Here we can notice that either adding the constant D or subtracting makes a shift in the graph whether it is vertically or horizontally. The graphs on the left represent a vertically shift. When D is positive, you have a shift in the graph upward the number units added and when it is negative, you have a shift downward on the y-axis. The graphs on the right represent a horizontal shift. When d is positive, you will have a shift to the left along the x-axis and when it is negative, you shift to the right.