

For this problem, we want look characteristics of a centroid. So we will start out by making an acute triangle.
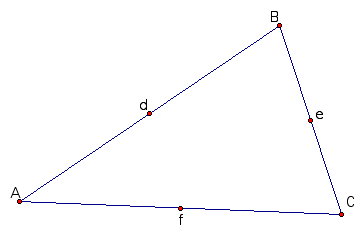
Now, we need to construct the midpoints of the triangle.
Next, each vertex of the triangle ABC will correspond its opposite midpoint hence creating the medians. For example, point d will map to the vertex c, point e will map to the vertex a, and point f will map to the vertex b.
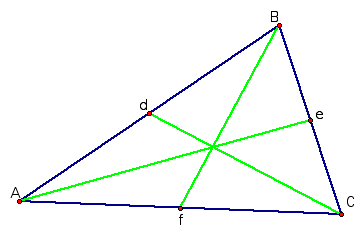
As you can see, each of the medians intersect at one point which we call the centroid.
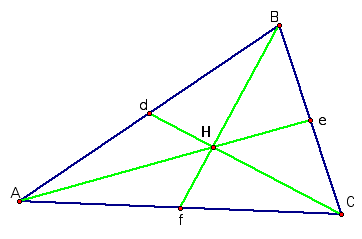
Now, if we calculate each segment, we will see that the ratios are the same.
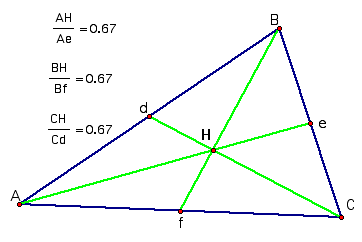
If we look at another ratio, we see that the following:
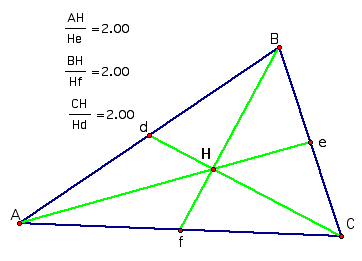
We see that all three ratios are 2 or 2 to 1.
So from this exploration, we know that the centroid divides the medians in a ratio of 2 to 1 of the triangle ABC.
PLAY HERE with Each of the vertices to see that ratios are unchanged!!