Barney is in the triangular room shown below. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB.
- Prove that Barney will eventually return to his starting point. - How many times will Barney reach a wall before returning to his starting point?
- Explore and discuss for various starting points on line BC, including points exterior to segment BC.
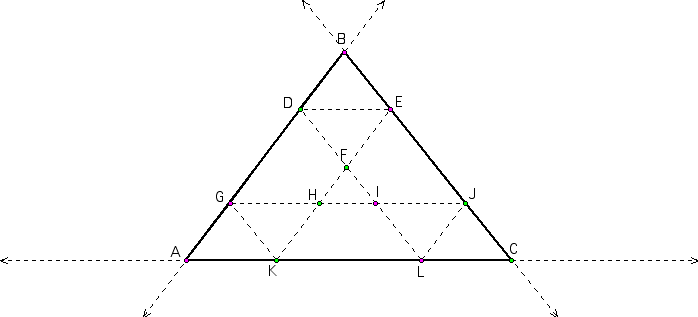
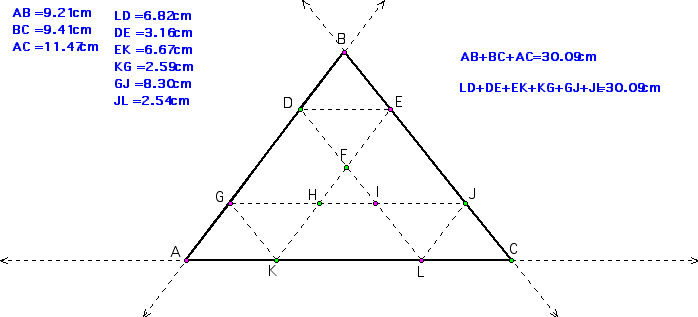
So, if Barney walk from a point on BC that is parallel to AC, the perimeter of the path of where Barney started is equal to the perimeter of the triangle ABC. Click HERE to move vertices to see that the perimeter remains unchanged.
And since we know that
, 
, and
, this implies that all the triangles
(
,
,
,
,
,
,and
) are similar to triangle ABC because
they have the same angle measurements.
Similarly, since 
,
, 
, 
, 
, 
are equal to each other, then 
.
So since 
and
, then 
. Likewise,
since 
and 
, then
and finally, since 
and
, then 
. Therefor,
the perimeter of ABC is equal to the perimeter of KEDLJG.
Lastly, if barney started walking outside the walls, then it would still be the same perimeter because the sides are still parallel to the triangle ABC. This exploration is very interesting and thought provoking. I see this being a good high school or middle school project.