
Features of a Pedal Triangle
To construct a pedal triangle, let ABC be any triangle. If any point P in the plane of the triangle, the triangle that is formed by the perpendiculars to the sides of ABC through P, the three points D, E, and F that are the intersections of the perpendicular lines and the sides of the triangle is the pedal triangle.
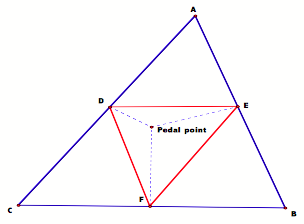
Suppose I use the same pedal point to find the pedal triangle of the pedal triangle. Our conjecture is that the third pedal triangle is similar to the original triangle.
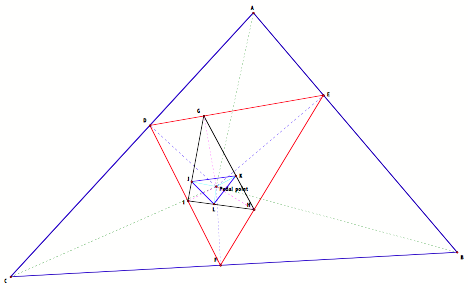
Proof: If we were to construct segments of the pedal point and the vertices, we notice that the sum of angles Ð DAP and ÐPAF is congruent to the sum of angles ÐKLP and ÐPLJ. That does not happen in any of the prior pedal triangles.
ÐDAP = ÐDEP yet, ÐPAE ¹ ÐPEF and ÐPAE = ÐPDE yet ÐDAP ¹ ÐPDF. Therefore, DABC ¹ ÐDEF. Similarly in triangle DGHI, though ÐKHP = ÐDAP, ÐPAE ¹ ÐPHL, and ÐPAE = ÐPIJ yet ÐDAP ¹ ÐLIP. Again, DABC ¹ ÐGHI. Within the third pedal triangle however, ÐDAP = ÐKLP, ÐPAE = ÐPLJ so the angle ÐA = ÐL, similarly, the angles ÐB = ÐJ and ÐC = ÐK¬
If you follow closely, you might notice that after the angle ÐA was divided into angles, one angle moves clockwise and the other moves counterclockwise. Since the figures are triangles, on the third move the two angles meet again to form the angle ÐA.
Altering the Pedal point
Because of the many possible triangles of the pedal point at different position, it is also call a cevian point.
If the pedal point were to be the centroid of the triangle DABC, the pedal triangle is within the original triangle. We have similar to the one above.
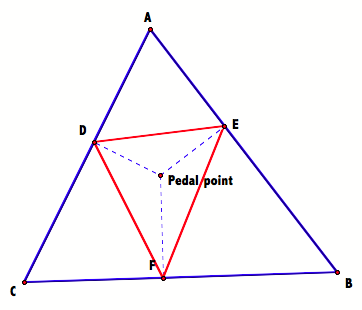
If the pedal point is the incenter of the triangle ABC, similarly to the centroid the pedal triangle remains inside the triangle ABC.
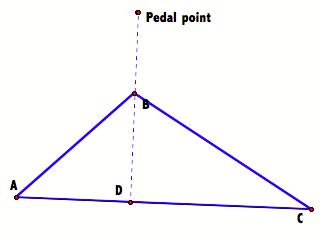
However, if the pedal point is the orthocenter, the pedal triangle is not always a triangle. For instance if the orthocenter, as the pedal point is nowhere on the interior of the triangle, we obtain a simson line.
With the circumcenter as the pedal point, the pedal triangle is always inside the triangle ABC at all times, even if the circumcenter is outside the triangle. To explore the pedal point at some other position, click here.
At many other position of the pedal point you will find the pedal triangle is nothing but a line. Why? That is because the vertices of the pedal triangle are perpendicular, and that is the definition of the simson line. To see it better, click here.