
EMAT 6600
Problem Solving
Exploring Bisector of an Angle of a Triangle
Notice, given any triangle ABC, if bisect one of its angles, the ratio of the adjacent sides are equivalent.
Proof: Suppose this is the given triangle
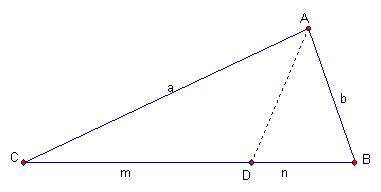
Due to the bisector m is to ADC as n is to ADB. By the property of reflectivity, AD = AD. So a is to ADC as b is to ADB. Thus, n/m = b/a. Click here to see.
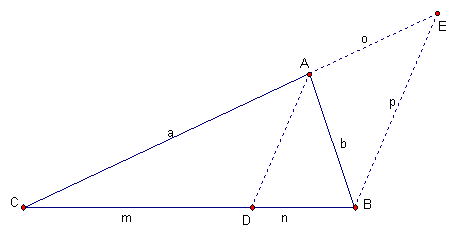
If drawn the bisector of the angle C, we then can state that (a + o) / (m + n) = r/s as depicted below:
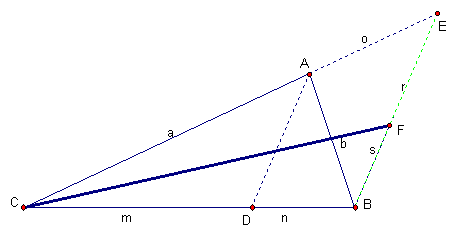
Also, r/s = t/u; thus by transitivity (a + o)/(m + n) = t/u. Hence, CAD is equivalent to CEB.