
EMAT 6600
Problem Solving
Carl’s Cone
Problem: How do
I make a pattern for a cone that is 12 inches tall and has a base diameter of
24 inches and a top diameter of 8 inches? Can you share the formula with me
please?
Solution: Let us try to depict this.
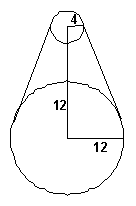
If we were to have an entire cone, we would be able to find the volume of the cone, and then subtract the missing part. So, let us construct the entire cone.
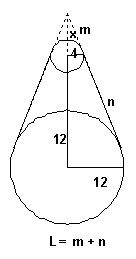
The volume of the entire cone is (1/3) p144(12 + x). The volume of the smaller cone is (1/3) p16(x). However we do need to know the length of slanted side. Using Pythagorean theorem, we have 144 + (12 + x)^2 = L^2. That is for the entire cone. For the smaller cone, however, we have 16 + x^2 = m^2. However I do not know what x is. Take notice that I have two right triangles. Using rationality, we have x/4 = (12 + x )/12.
Consequently, x = 6. Hence, L = sqrt(468) inches, m = sqrt(52) inches.