
EMAT 6600
Problem Solving
Concurrence Theorems
Prove: The perpendicular bisector of the sides of a triangle meet at a point, which is equally distant from the vertices of the triangle.
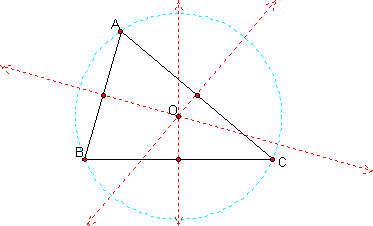
Proof:
The triangle ABC is inscribed in the circle O. The points A, B, and C are on the circle. The segments OA, OB, and OC are the radii of O. Hence, the perpendicular bisectors of the sides of a triangle meet at a point that is equidistant from the vertices of the triangle.
Click here to se a construction.
Prove. The bisectors of the angles of a triangle meet at a point that is equally distant from the sides of the triangle.
Proof : Consider the triangle ABC with its angle bisectors
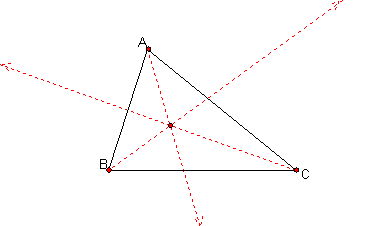
If we inscribe a circle inside the triangle, where the circle is tangent to the sides of the triangle, we have
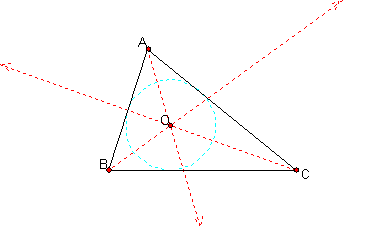
Notice that the points of tangency on each side and the point of concurrency make the radius of the circle.
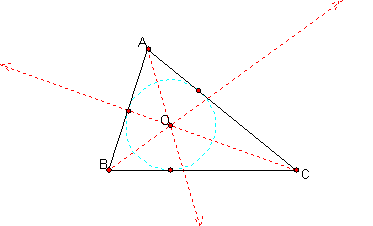
Thus, the sides are equidistant from the point of concurrency of the angle bisectors.
Click here to construct an incircle.
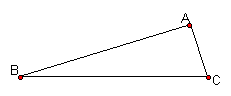
Prove. Let the sides of a triangle be extended so as to indicate the external angles. The bisectors of the external angles on one side of a triangle and the bisector of the opposite internal angle are concurrent.
Consider the triangle ABC
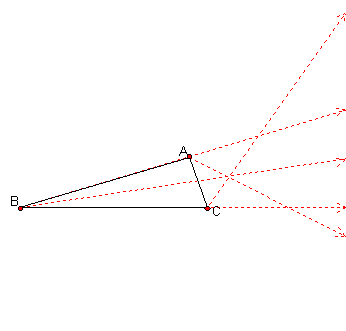
If we construct a parallel line to BC that passes through A and a parallel line to BC that passes through C, we obtain
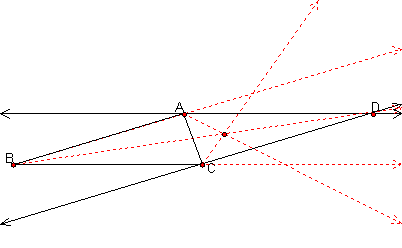
A parallelogram ABCD.
Consider triangles ABC and ADC
ÐADC º ÐABC. So, the angle bisectors are the same. We know that the angle bisectors of a triangle are concurrent. So, the bisectors of ÐABC, ÐDAC, and ÐDCA are concurrent.
Click here to construct an excircle.