
EMAT 6600
Problem Solving
Distance Survey Problem
In conducting a land survey, the following problem arose. There were two points A and B along a road and points C and D off the road along the respective perpendiculars to the road at A and B. There were buildings on the property that prevented direct measurement of the distances along BD and AC. Measurements, however, could be made for AD, BC, and AB as follows:
AB = 240 yards
AD = 260 yards
BC = 300 yards
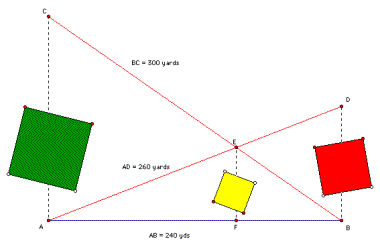
A light pole is to be installed at point E, the intersection of CB and AD. How far will the pole be from the road? That is what is the distance EF? Again, an existing building blocks direct measurement.
Solution:
Using the Pythagorean theorem, AC = 180 and BC = 100
Now, consider the trapezoid ABDC, where AC || BC and AD and BC are the diagonals of the trapezoid.
To find the length of EF, we use the harmonic mean (H), which give the length of the segment that passes through E and is parallel to both AC and BD.
H = (2*100*180)/100 + 180 = 128.57 yards
Since EF is only a half of that, EF = 64.29 yards.