---

EMAT 6600

Problem Solving

---

Excircles

Given triangle ABC with side lengths a, b, and c. Let circle O be an excircle and let X, Y, and Z be its points of tangency, as shown.

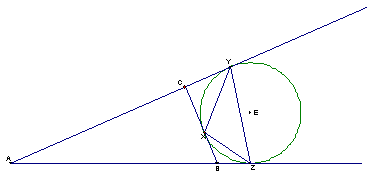
Prove that AC + CX is the semiperimeter of triangle ABC.

Click here to construct an excircle.

Given that the circle E is the excircle of the triangle DABC, the bisectors of the angles ÐYCX and ÐXBZ are concurrent at E.

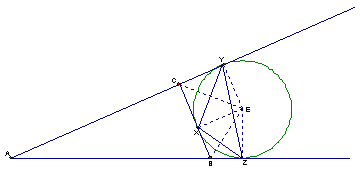
Observe that triangles DEXB and DEZB are congruent due to SAS. Using the Pythagorean theorem, notice that segments CY and CX are congruent and segments XB and BZ are congruent as well. Since, CY + BZ = CB, the perimeter of the triangle,

P = AY + AZ. Now, we must show that segment AZ is the semiperimeter. Since the excircle is opposite angle ÐA, the bisector of the angle passes through the center of the excircle.

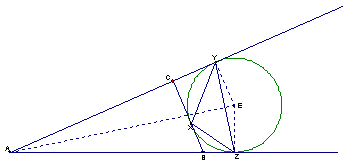
Again, using Pythagorean theorem, the segments AY and AZ are congruent. Thus, the segment AY is the semiperimeter of the triangle DABC. We know that AY = AC + CY.

We also know that CY = CX. By substitution, AY = AC + CX, the semiperimeter of the triangle DABC.¨

Prove that triangle XYZ is obtuse, that is, that the triangle determined by the points of tangency of an excircle is always obtuse.

Consider the following

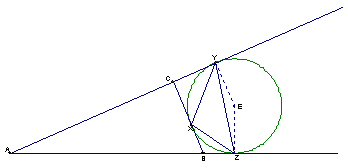
Observe that triangles YEC and XEZ are isosceles triangles. Hence, angles ÐXYE and ÐYXE are congruent; similarly, angles ÐEXZ and ÐEZX are congruent as well. Consequently,

ÐYEX = 180 - 2ÐYXE; ÐXEZ = 180 - 2ÐEXZ; ÐYEZ = ÐYEX + ÐXEZ;

ÐYXZ = ÐYXE + ÐEXZ; ÐYEZ = 180 - 2ÐEYZ.

So

ÐYXE = 90 – ½ (ÐYEX); ÐEXZ = 90 – ½ (ÐXEZ)

ÐYXZ = 90 – ½ (ÐYEX) + 90 – ½ (ÐXEZ)

= 180 – ½ (ÐYEX + ÐXEZ)

= 180 – ½ (ÐYEZ)

= 180 – ½ (180 - 2ÐEYZ)

= 180 – 90 + ÐEYZ

= 90 + ÐEYZ

Angle ÐYXZ > 90. Thus, triangle DYXZ is an obtuse triangle.¨

---

Return

---