
Geometry Exploration
by
Larousse Charlot
Exploring the point D traveling the given triangle ABC, I notice that the point travels each side of twice before return to its original location. That is true for every starting position of D except one, unless it is one of the vertices.
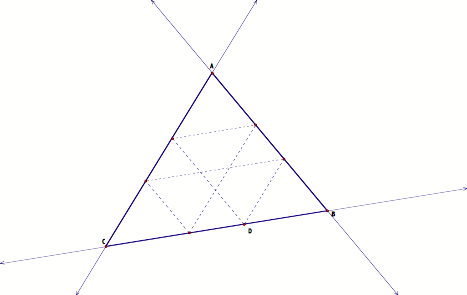
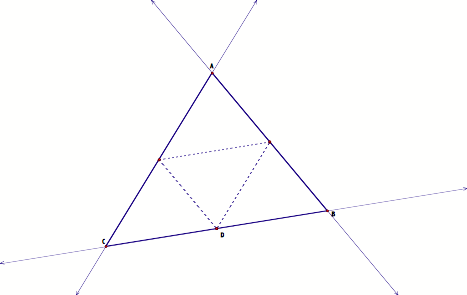
That particular one point seems to be the midpoint of the segment of the side that the point D is traveling. In order to verify this conjuncture, I construct the midpoint of each segment of the given triangle ABC. See it here.
As you can observe, at the midpoint the traveling point D only travels each side of the given triangle is one time before returning to its starting point.
At any other starting point, besides the midpoint, we have a hexagon. Try it here.
Now, if we just use our eyes to observe the triangle that is formed by the path of D traveling the sides of the triangle ABC at the midpoints of each of the segments, we can safely state that the formed triangle is a median triangle of the given triangle. However, if the given triangle is an equilateral triangle, the path traveled by the point D is also the orthic triangle of the given triangle.
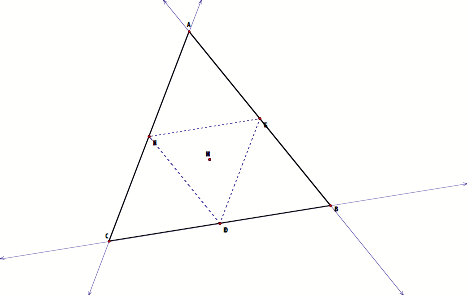
In order to find that, I constructed the orthocenter of both triangles and shape the triangle so that the orthocenter for both triangles is the same point. See it here.
What I also observe is that when the three lines that are parallel to the bases of the given triangle intersect, they intersect at the centroid. The centroid is same for both triangles. Feel free to construct the centroids yourself (here, despite the shape of the triangles).
The perimeter of the Hexagon
At any position of the point D inside the given triangle, the perimeter of the hexagon is congruent to that of the triangle, with the exception of the midpoint at which we do not have a hexagon. When D is outside the triangle, however, the perimeter of the hexagon accrues of course. The sides of the hexagon that are parallel to the bases of the triangle share the same ratio, as to the base of the triangle : the side of the hexagon (parallel to the base). As the hexagon grew larger so is the ratio. However, I do not think this is not quite the way to go because the ratio change as the figure gets bigger. We could consider the directions in which each segments go in order to find the directed perimeter, which would be congruent to the perimeter of the triangle, but I wish otherwise( see how the point moves on the hexagon from inside and outside to get the sense of direction of the segments). Therefore, more research and observation are to be done on this matter.