

EMAT 6600
Problem Solving
Fly and Spider
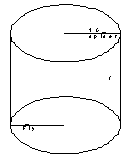
A room has the shape of a right circular cylinder with radius r = 10 ft and height h = 8 ft. A spider is on the room's ceiling, 7 feet from and directly to the east of the ceiling's center. A fly is on the room's floor, 7 feet from and directly to the west of the floor's center. Determine (analytically or numerically) the minimum distance the spider would have to crawl in order to reach the fly
Solution:
Let us construct this room.
Knowing that the shortest distance is a straight line, consider the room being flat as a rectangle and the circle. There are many possibilities.
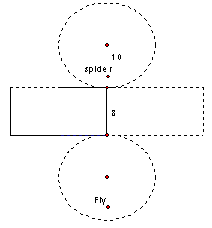
The shortest line the fly would have to crawl is when the circles are aligned. When the circles are in the opposite end we have this.
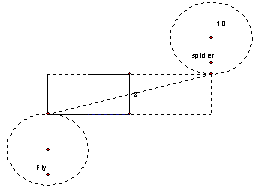
In general, the fly would have to crawl three feet on the radius and cut through the rectangle, and crawl seven feet on the other radius. Click here to see it.