EMAT 6600

Problem Solving

 

 


Minimum Length

 

Problem:  An attic room is 54 ft wide and 8 ft high. What is the minimum length of tilted roof needed to cover the room and find its length?  It is depicted as follow:

 

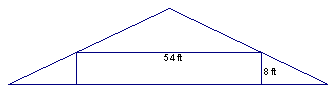
Solution:  realize that we have an isosceles triangle.  So, the height would the segment the opposite vertex and the midpoint of the base.

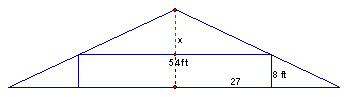
Due to congruent triangles, we have congruent angles.

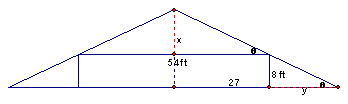
From there, we know that (8 + x)2 + (27 + y)2 = z2, where z is the length of the tilted roof.  This equation does not help much.  Let z = z1 + z2.  Using trigonometry, z1 = 27/cos q and z2 = 8/sin q.  Now, z = (27/cos q) + (8/sin q).  Since we want to find the minimum here, we use calculus to the derivative of the equation.  First, let us simplify this using definition of trigonometry functions.  z = 27 sec q + 8 csc q.

z’ = 27 sec q tan q - 8 csc q cot q = 0

                               27 sec q tan q = 8 csc q cot q

if multiply both sides of the equation by cot q cos q, we obtain

                                                 27 = 8 cot3 q

                                                3/2 = cot q

set this result in a triangle we that cot-1 (3/2) = Ö13.

So, z = 27*(Ö13)/3 + 8*(Ö13)/2

         = 13Ö13,  so, 26Ö13 is needed to cover the room.

Return