
EMAT 6600
Problem Solving
Mirror Image
Suppose a mirror was to be placed flat on a wall that is perpendicular to the floor. What is the shortest mirror a 6 feet tall person could use so as to be able to see an image in the mirror from the top of the head to the toes? Assume the person is standing 5 feet from the mirror.

Let us call this 6 feet tall person Henry. Assuming Henry is looking at the image of his entire body. Suppose that Henry’s head is aligned with the top of the mirror, considering that the mirror has no frame. So, we know that his image is 10 feet away from where he is. Just like this.
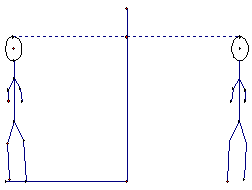
the mirror has to be a certain length in order for him to see his toes. However, the mirror is not 6 feet tall. Since his reflection is the same height as he, let x be an integer such that 0 < x < 6. So, we end up with a picture of this manner.
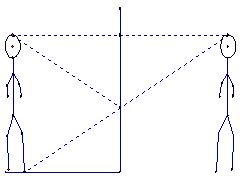
Knowing the distance of the Henry’s image from himself implies that the length of the diagonal segment to be 2sqrt(34). Because of the sets of isosceles triangles, the length of the segment from Henry’s head to the bottom of the mirror is sqrt(34). Using the Pythagorean theorem, we obtain that the length of the mirror 3 feet tall.