
EMAT 6600
Problem Solving
Problem with Cylindrical Tanks
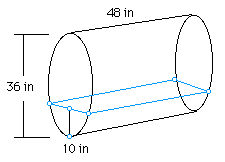
This problem was seriously proposed to one of my EMT 725 students by their Superintendent. At the Superintendent's home the furnace used fuel oil stored in an underground tank. It was known that the tank was installed level on its side and that it was 36 inches in diameter and 48 inches long. Using a stick dipped through the fill tube, the superintendent determined he had 10 inches of oil in the tank. He really did NOT want to know how to calculate the amount of oil. He knew from experience that it was February and he would need about 40 gallons of oil to finish the season. Would he have enough oil?
Solution:
In order to find the volume that is occupied by oil, first we need to find the area the oil occupies on the circle.
What we know: radius = 18 in, height = 10 in, and length of the cylinder is 48 in.
Let us focus on the circle. Consider the following:
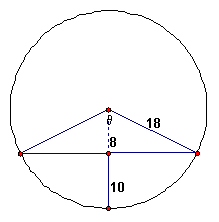
Now, we need to know the length of the base of the triangle. Using the Pythagorean theorem, we have the length of the base equal to 32.25 in. That is because we have an isosceles triangle, the altitude is also the perpendicular bisector. The area of the triangle AT = 258 in2. The area of the sector of the circle is ½ qr2. However, we are yet to know the value of q. Using the laws of cosine, q = 2 cos-1(4/9) = 2.22. Hence, the area of the sector is 359.64 in2. Consequently, the area occupied by the oil on the circle is area of the sector minus the area of the triangle, which is 101.64 in2. With that, we calculate the volume by multiplying the result by 48 in and 2, which equals 9757.44 in3. As given, there are 231 in3/gallon. So, he has 42.24 gallons of oil in the tank. Given that he would need 40 gallons to finish the season; I would let him know that he is safe for the rest of the season.