
Fibonacci Sequence
Using Spreadsheet
by
Larousse Charlot
The Fibonacci numbers is defined by the following:
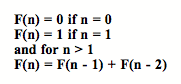
The Fibonacci numbers are named after Leonardo of Pisa, who was also known as Fibonacci. However, that was not the first time the Fibonacci numbers were discovered. They were described many years prior to Leonardo in India.
Nonetheless, for our exploration of spreadsheet, we are defining the Fibonacci sequence as follow:
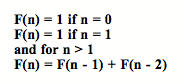
This is the sequence in the spreadsheet of Excel
|
n |
F(n) |
|
0 |
1 |
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
4 |
5 |
|
5 |
8 |
|
6 |
13 |
|
7 |
21 |
|
8 |
34 |
|
9 |
55 |
|
10 |
89 |
|
11 |
144 |
|
12 |
233 |
|
13 |
377 |
|
14 |
610 |
|
15 |
987 |
|
16 |
1597 |
|
17 |
2584 |
|
18 |
4181 |
|
19 |
6765 |
|
20 |
10946 |
|
21 |
17711 |
|
22 |
28657 |
|
23 |
46368 |
|
24 |
75025 |
|
25 |
121393 |
|
26 |
196418 |
|
27 |
317811 |
|
28 |
514229 |
|
29 |
832040 |
|
30 |
1346269 |
|
31 |
2178309 |
|
32 |
3524578 |
|
33 |
5702887 |
|
34 |
9227465 |
|
35 |
14930352 |
|
36 |
24157817 |
|
37 |
39088169 |
|
38 |
63245986 |
|
39 |
102334155 |
|
40 |
165580141 |
|
41 |
267914296 |
|
42 |
433494437 |
|
43 |
701408733 |
|
44 |
1134903170 |
|
45 |
1836311903 |
If we were to look at the ratio of F(n) to F(n – 1), we would have
|
n |
F(n) |
F(n)/F(n-1) |
|
0 |
1 |
1 |
|
1 |
1 |
1 |
|
2 |
2 |
1 |
|
3 |
3 |
2 |
|
4 |
5 |
1.5 |
|
5 |
8 |
1.666666667 |
|
6 |
13 |
1.6 |
|
7 |
21 |
1.625 |
|
8 |
34 |
1.615384615 |
|
9 |
55 |
1.619047619 |
|
10 |
89 |
1.617647059 |
|
11 |
144 |
1.618181818 |
|
12 |
233 |
1.617977528 |
|
13 |
377 |
1.618055556 |
|
14 |
610 |
1.618025751 |
|
15 |
987 |
1.618037135 |
|
16 |
1597 |
1.618032787 |
|
17 |
2584 |
1.618034448 |
|
18 |
4181 |
1.618033813 |
|
19 |
6765 |
1.618034056 |
|
20 |
10946 |
1.618033963 |
|
21 |
17711 |
1.618033999 |
|
22 |
28657 |
1.618033985 |
|
23 |
46368 |
1.61803399 |
|
24 |
75025 |
1.618033988 |
|
25 |
121393 |
1.618033989 |
|
26 |
196418 |
1.618033989 |
|
27 |
317811 |
1.618033989 |
|
28 |
514229 |
1.618033989 |
|
29 |
832040 |
1.618033989 |
|
30 |
1346269 |
1.618033989 |
|
31 |
2178309 |
1.618033989 |
|
32 |
3524578 |
1.618033989 |
|
33 |
5702887 |
1.618033989 |
|
34 |
9227465 |
1.618033989 |
|
35 |
14930352 |
1.618033989 |
|
36 |
24157817 |
1.618033989 |
|
37 |
39088169 |
1.618033989 |
|
38 |
63245986 |
1.618033989 |
|
39 |
102334155 |
1.618033989 |
|
40 |
165580141 |
1.618033989 |
|
41 |
267914296 |
1.618033989 |
|
42 |
433494437 |
1.618033989 |
|
43 |
701408733 |
1.618033989 |
|
44 |
1134903170 |
1.618033989 |
|
45 |
1836311903 |
1.618033989 |
As you can observe, as n increases the ratio of F(n) : F(n – 1) approaches the golden ratio (j) number that is defined by
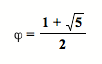
So, the ratio of F(n) : F(n – 1) is bounded by the golden ration. Hence, we can have a closed formed expression for the Fibonacci numbers.
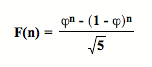
An equation is said to have a closed form expression if and only if the equation has at least one solution that can be analytically expressed as a bounded number of a certain function, in this case the golden ratio.
Consider the ratio of F(n) : F(n – 2). I think an addition to the golden ration will occur because F(n – 2) = F(n – 1 – 1). See if I am right here, I could be wrong.
If redefined our sequence such that we F(0) = 1 and F(1) = 3, we would have the Lucas number, due to Francois Edouard Anatole Lucas, which is defined as
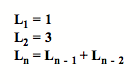
which follow the same path as Fibonacci sequence, and have the same ratio.
Golden Ratio
Suppose we have a line segment that is divided into two no equal parts. If the ratio of the whole segment to the larger part of the segment is equal to the ratio of larger part of the segment to the smaller part of the segment, the ratio is a golden ratio. Algebraically, we have
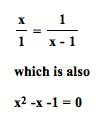
from which we obtain j.