
Class Page
Of
Larousse Charlot
The Centroid
Of
A triangle
First, let us construct a triangle. In order to do that, we must have three non-collinear points. Let the three points be A, B, and C as follows:
Now, let AB, BC, and AC be segments. Using GSP, I construct the segments of the points.
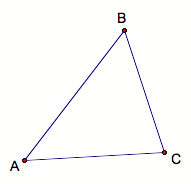
What you see here are rays emanating from each point to form angles. The intersection of the angles interior defines the triangle. Hence, we have the triangle Æ ABC.
Let there be three distinct points, M, N, and O lying on the segments AB, BC, and AC such that we have A*M*B, B*N*C, and A*O*C, which means the points M, N, O are between AB, BC, and AC respectively, such that Am Å MB, BN Å NC, and AO Å OC.
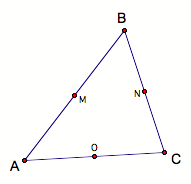
So, we can state that the points M, N, O are midpoints of the segments AB, BC, AC respectively, by definition.
Let MN be a segment. Since, the segment MN joins the midpoints of AB and BC, MN is parallel to AC, and MN is half of AC, by definition of mid-line of a triangle.
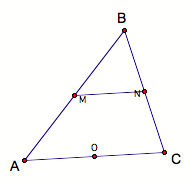
Let AN, MC be segments, then we have the point P as the intersection of AN and MC.
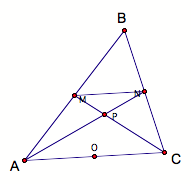
So, here we have
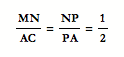
Which implies that
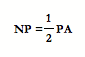
Therefore, NP is a third of AN.
The lines AN and CM are midlines of triangles Æ BAC, and BCA respectively.
Similarly, if construct the segment BO
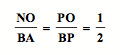
If the segment BO passes through P, then P is not the centroid.
Behold:
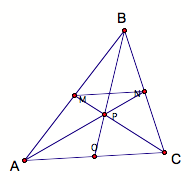
So, we can conclude that the intersection point P is the centroid of the triangle Æ ABC.
The point P is the Centroid of the triangle Æ ABC, and the point P is placed two thirds of the segments AN, BO, and CM from the vertices, A, B, C respectively.
The Centroid of the triangle will always remain at the center of the triangle no matter what shape the triangle is changed to. See Triangle (play with it).
Using GSP, we would follow each step as stated and weÕd obtain the figures that have been depicted above. The diagrams for this site were done using GSP.
Students would be at ease if the steps of the proof were constructed in front of them, steps by steps.