
EMAT 6600
Problem Solving
Problem: Let S be a sequence of consecutive positive integers whose terms have a sum of 2007. Find all such sequences S, and prove that you have found them all. (Do not include the trivial sequence consisting of 2007 alone.)
Solution
Reasoning: If I have three consecutive integers and choose x as the initial integer, the three integers will be x + (x +1) + (x + 2) = 2007. As a result, I have x = 668. That is for only three consecutive integers. Now, suppose that I have n integers. That is x + (x + 1) + … + (x + (n – 1)) = 2007. Since I have n terms, I might need to solve for x. Thus, nx + {1 + … + (n – 1)} = 2007. This is equivalent to nx + {(n – 1)(n – 1 + 1)}/2 = 2007. From here, we can solve for x, where n represents the number of terms. Thus, the general formula for finding n consecutive integers with their sum being 2007 is
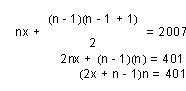
From there, if a particular n is chosen, one can solve for x. However, that does not prove that all the consecutive numbers are found. So, to find all the consecutive numbers that the sum is 2007, we can consider the fact that n is factor of 4014 and 2x + n –1 is also a factor. So, if we consider the factors of 4014, they are 2 and 2007, 6 and 669, 18 and 223. Because each of the factors could be n, there must be 2007 consecutive integers that add up to 2007, including negative integers (at x = -1003). But if we wish to only have positive consecutive integers, we can have a maximum of 18 integers.