
EMAT 6600
Problem Solving
Constructing the Squarable Lunes
Hippocrates of Chios constructed the first three Lunes. The way he had done it was rather ingenious. A lune is the convergence of two concave acrs, as depicted below:

Now, this is an irregular shape. How does one go about finding its area.
Observe that the two arcs are of two different circles. If we construct the sectors of these circles, we might be able to differ the areas of the two sectors.
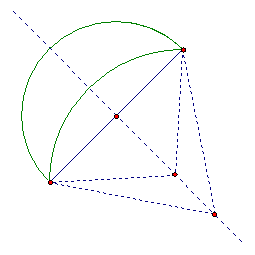
Let us label the figure for a better sense.
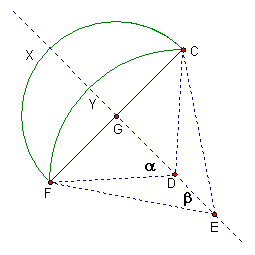
One of the circles has a radius GD and the other has a radius GE. For our ease let GD = r, GE = R, sector FXCD be S1, and sector FYCE be S2. So, the areas of the sectors are S1 = ar^2 and S2 = bR^2. So the area of the lune FXCY is AL = AFXC - AFYC, where AL is the area of the lune, similarly with AFXC and AFYC. To find the AFXC, we must take in account the sectors. So, AFXC = S1 – AT1, where T1 is triangle FCD. Dealing with unit circle, we can use polar coordinates to find the area of a triangle is (r sin q)(r cos q). In our case, we would have (r sin a)(r cos a).
By trigonometry identities, r^2(sin a cos a) = (½)r^2sin(2a).
So, AFXC = S1 - (½)r^2sin(2a). Similarly AFYC = S2 – (½)R^2sin(2b). By substitution, we have AFXC = ar^2 – ½ r^2*sin(2a), and AFXY = bR^2 – ½ R^2*sin(2b). Consequently,
AL = ar^2 – ½ r^2*sin(2a) - bR^2 + ½ R^2*sin(2b). Since we are dealing with unit circles, Let ar^2 = bR^2. we then obtain,
AL = ½ R^2*sin(2b) - ½ r^2*sin(2a).
Consider the circle O.

Build two diameters of the circle, and construct a triangle with a fourth of the circle just like a fantastic four, as done below.
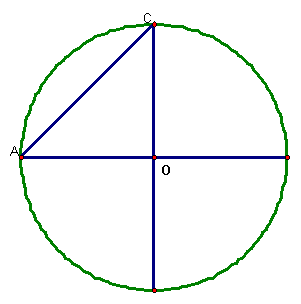
construct a circle with diameter of AC
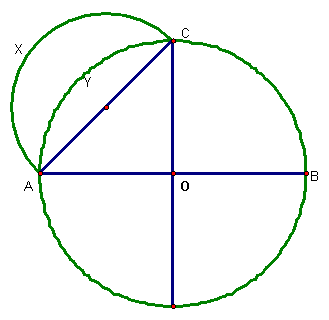
What is the area of yellow region?
Consider DABC being a right triangle, being in half of a circle. So, AB^2 = AC^2 +AB^2. Take notice that AC = CB; thus AB ^2 = 2AC^2. Hence, the area of the semicircle ACB = 2(area of AXC).
The area of AXC = the area of AYCO. So, the area of AXCY = area of AXC – area of AYC, and area of AYC = area of AYCO – area of DACO . Then area of AXCY = area of AXC – area of AYCO + area of DACO. Since the area of AXC = are of AYCO, area of AXCY = area of DACO.
We can take that transfer to what would happen to the lune that would be on CB. The triangle ACB would equal the sum of the two Lunes.
To construct the next lune, consider the circle O with the triangle ACB. Construct the bisectors of the angles and construct an arc with AIB where I is the incenter of the triangle ACB. Now show that the area of the lune is congruent to that of triangle ACB.