
EMAT
6600
Problem
Solving
Problem: In non-cyclic quadrilateral ABCD, points E,F,G,H are the circumcenters of triangles ABD, BCD, CDA, and CAB, respectively. The diagonals of quadrilateral EFGH meet at point P. Prove that AP ≈ CP and BP ≈ DP.
Solution: Click here to see construction
Now using our knowledge of geometry, apply some of them to start our proof. Let us bring the triangle APC away from the figure.
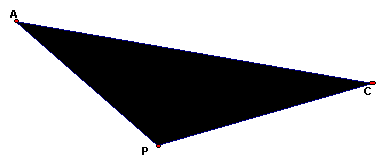
If we were to construct the angle bisector of angle P, the features of a bisector can be helpful.
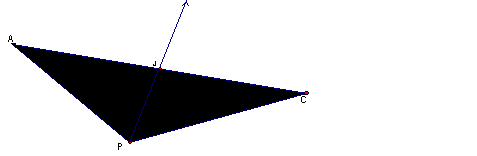
By the properties of a bisector, we can safely state that AJ = JC and that PJ ┴ AC. By the properties of similar triangles SAS, we see that AP = PC. Similarly, BP = DP