
All About Sine

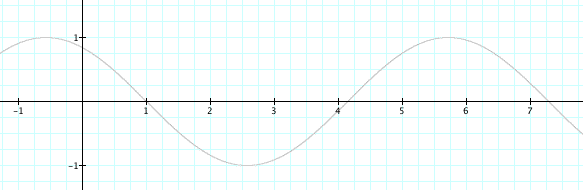
Before we can begin to explore how altering a, b, and c we should examine what the graph of sine looks like. So here is a graph of sine.
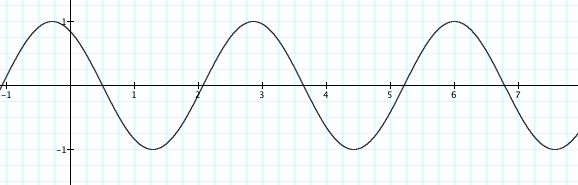
Now here is a graph of y = a sin(bx + c).
The reason the graph has shifted is because now it has variables and the variables change the way that the graph looks. All the variables are equal to 1 in the graph above.
We should know a few things about the graph of sine before we start examining how each variable changes the graph. Sine is a periodic graph, which is a graph that repeats itself over a certain period. Sine repeats itself every 2 pi distance. Its domain is the set of real numbers from negative infinity to infinity and its range is -1 to 1.
Now lets see what happens when you alter the value of the variable a and the variables b and c are equal to 1.
Let's let a = 1, 1.5, 2, 0, -1, -1.5, -2 and .5.
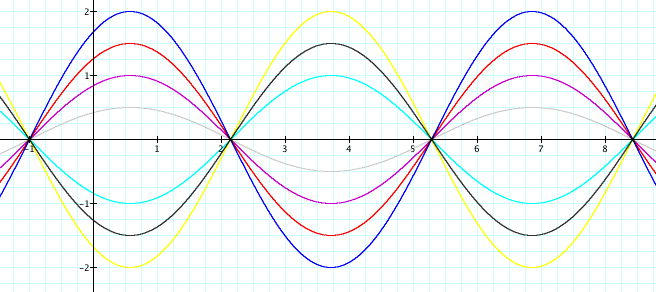
As you can see from the graphs, the length of the curve is not altered, but the height or amplitude of the curve is what is changed when a is manipulted. Amplitude is the height of the curve. As a increases, the height of the curve gets larger. When a is negative, the curve is reflected over the x-axis. When x is less than 1, then the curve gets closer to the x-axis. As you can see, the sine function where a = 0 does not appear because multiplying it by 0 makes the function equal 0 and so it cannot be seen on the graph.
Now let's look at what happens when the variable b is changed, and a and c are equal to 1.
Let's let b = 1, 2, .5, 0, -.5, -1, and -2.

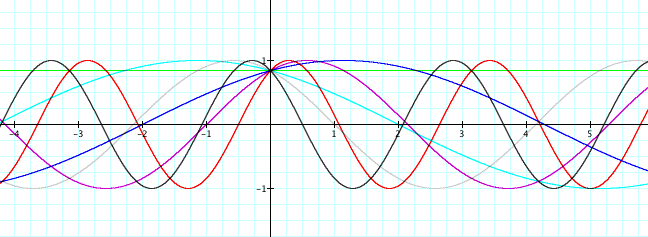
With all these lines going everywhere, it is hard to see what is going on when the b variable changes. So lets look at each individual graph seperately.
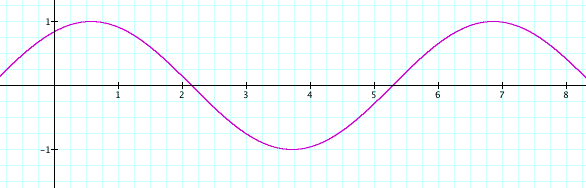
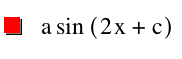
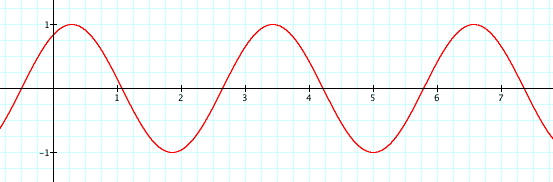
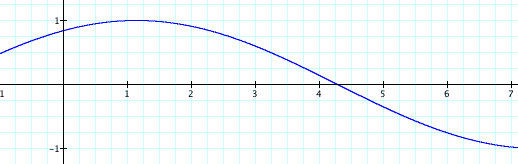
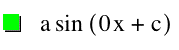
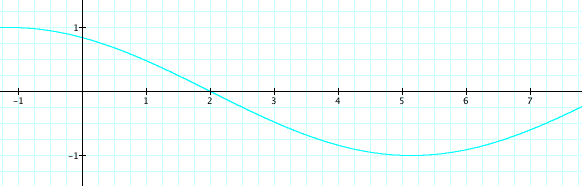
When you are looking at the different graphs with the variable b changing, then you see that as b increases the number of curves within the cycles increases. When b = 1, there is one full cycle of curves in the interval, but when you look at when b = 2 there are two full cycles of curves in the interval. And as b decreases, the curve gets flatter and looks more toward a straight line. Therefore we discover that b corresponds to the number of cycles within one interval of the sine curve.
When b = 0, that means that there are no x's and that the we are taking the sin (1) and that is why it is a straight line. If c was not equal to 1 and c was equal to 0, then we would take sin (0), which would be the x-axis.
Now let's look at what happens when we change the variable c, when a and b are equal to 1.
Let's let c = 1, 2, .5, 0, -.5, -1, and -2.
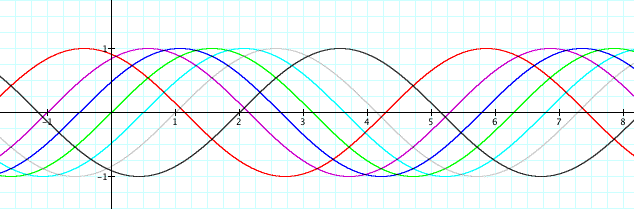
With all the lines everywhere, it is hard to see what goes on when c changes, so let's look at each individual graph.
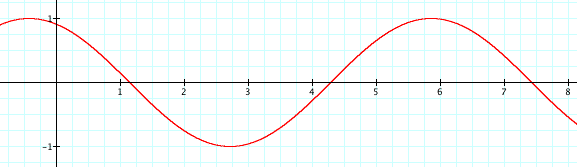
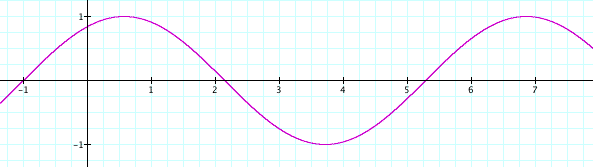
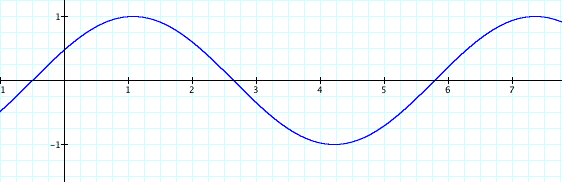
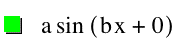
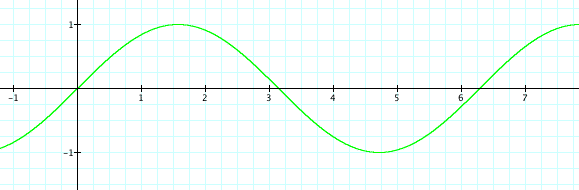
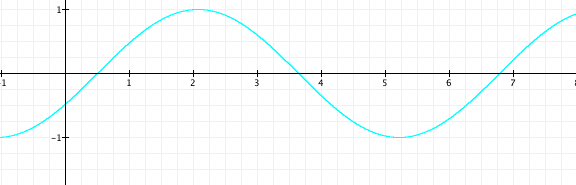
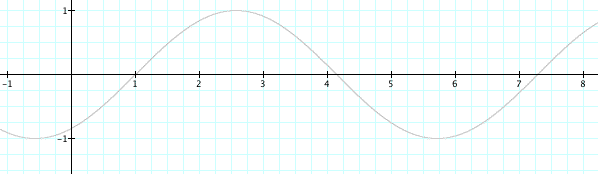
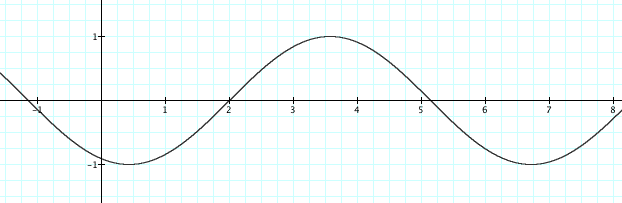
As c changes, the placement of the graph shifts. When c is negative the graph shifts to the right, towards the positive side of the graph, and when c is positive the graph shifts to the left, or the negative side of the graph. This pattern will continue for all values, both negative and positive.
You can explore further and see what happens when you change all three variables at the same time.
By Carolyn Amos