

Investigate
When a and b are equal, and k is an integer, this is one textbook version of the "n-leaf rose." We can compare with
for various k. What if cosine is replaced with sine?
First, what is a polar equation?
A polar equation of a curve is usually expressed in polar coordinates and written with r as a function of theta. These equations may show different forms of symmetry around the axes.
First let's plot the original graph that we were given to investigate.
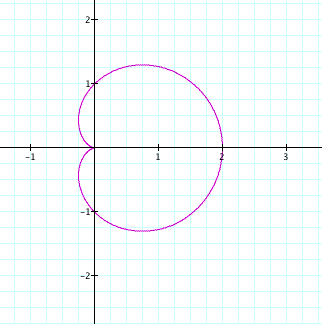
Now what will the graph look like if a and b are equal in the equation and k remains the same in each equation?
We notice that as a and b increased, the size of the petals increased. They remained in the same place, but grew as a and b increased.
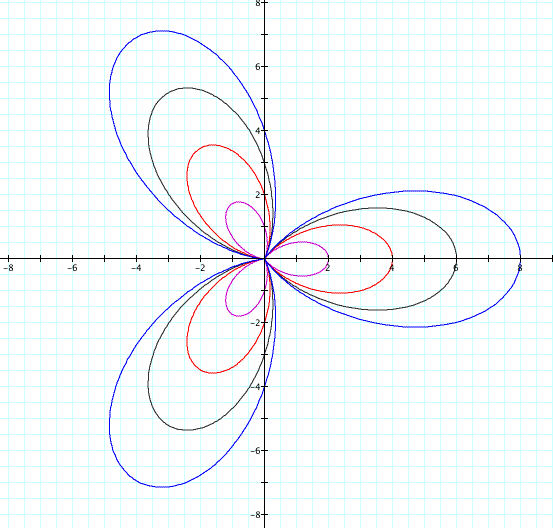
Now what if we only change k, leaving a and b constant at 2, what happens to the graph?
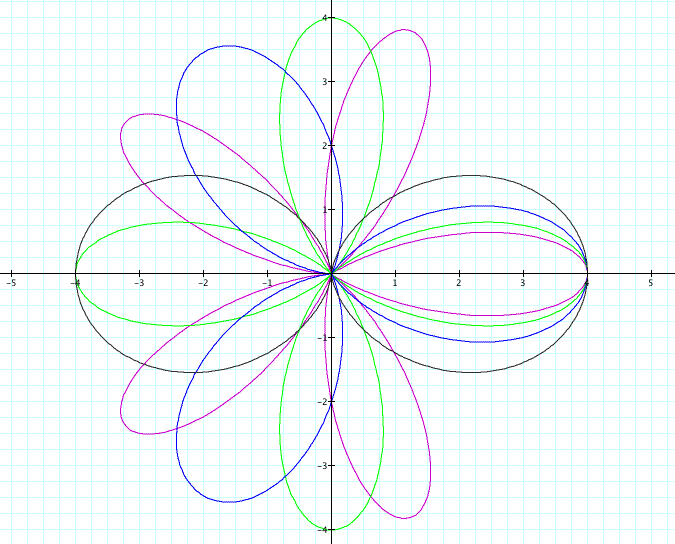
We can see that if k is an integer, that the number of petals on the rose depends upon the value of k. All the petals are the same length and the number of petals is the only thing that varied, because k was the only variable we altered.
What happens if a and b are odd?
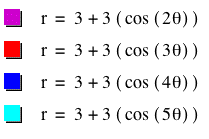
As we can see, nothing changed except the length of the leaves. Therefore we can assume that a and b affect the size of the leaves. We can tell from the graph above and the previous graph, that the length of the leaves is (a + b). When both a and b are 3, then all the leaves have a length of 6.
Let's continue investigating to see if we are correct.
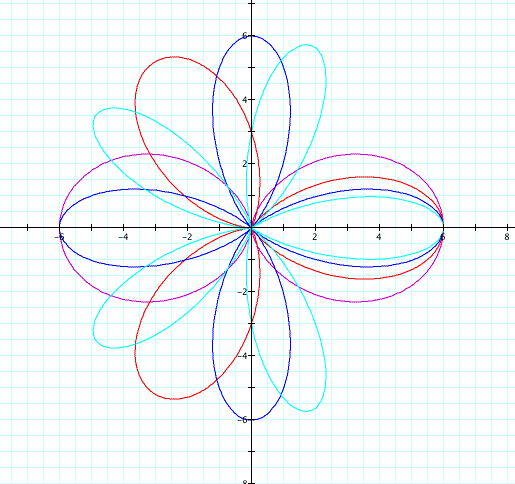
Now what happens when we change b, leaving a and k constant?
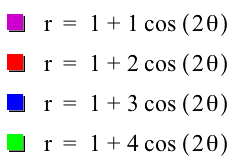
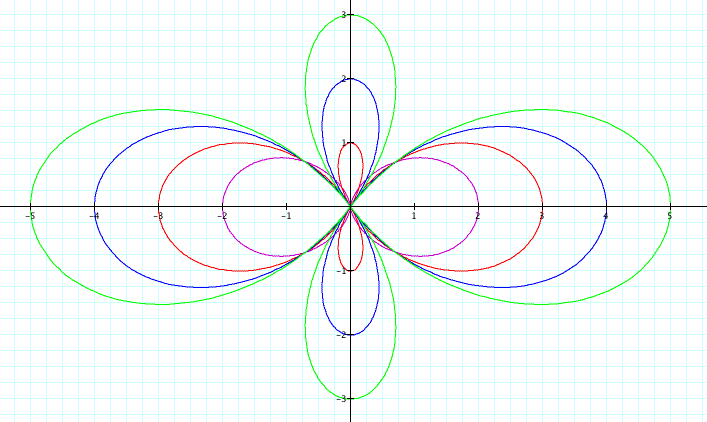
As b varies, the length of the petals increases as well. The variable b represents the length of the petals of the rose. As b increases, the length of the petal gets larger and larger. But if both k is even and b is even, the a 2k-petaled rose is prodiced. If k is odd and b is either even or odd, the a k-petaled rose is produced.
Now what happens when we change a, leaving b and k constant?
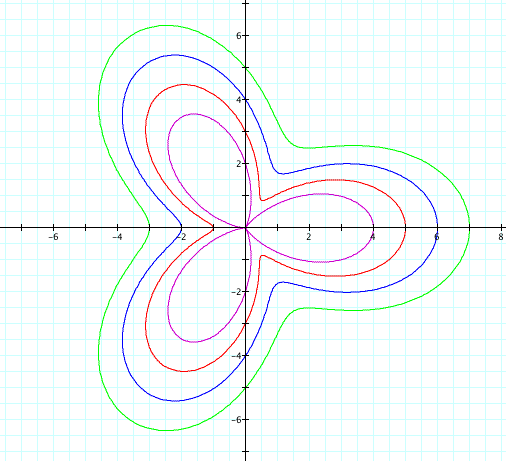
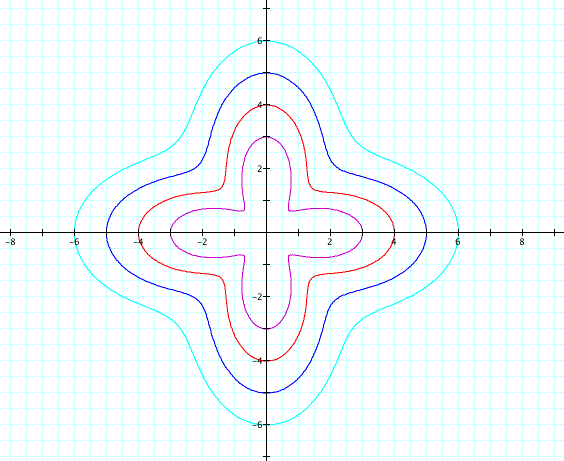
The first thing we notice is that the roses do not close in at the center of the graph. As a increases, the size of the petals have become larger. We can see that the length of the petals is a+b and that the difference between and b will end up being the difference in size of the smaller and larger set of leaves.
Click here to see an animation of a 15 petaled rose, where n = k, and k is varying among the integers between 1 and 15.
Now let's compare with the equation:
Let's check out what that equation looks like.
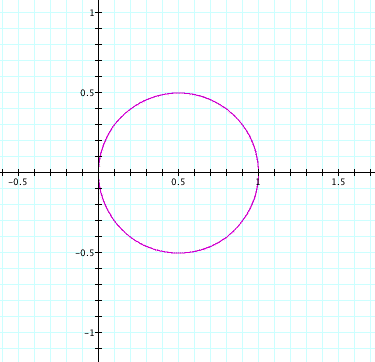
Let's put some different numbers in for k and see what happens.
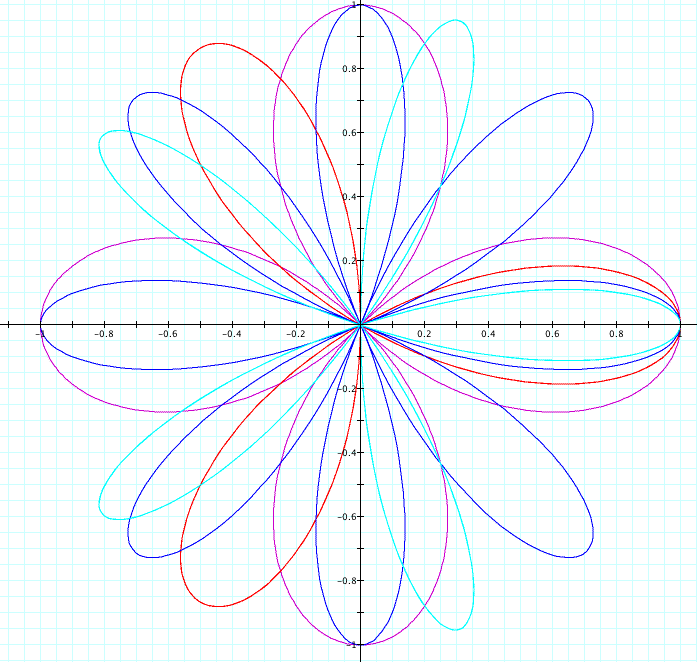
Now let's change cosine to sine and see what happens.
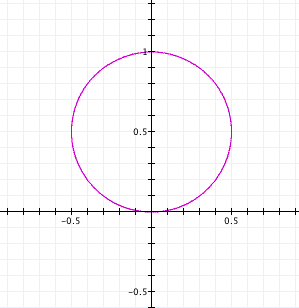
Now let's change the value of k in sine and see what happens.
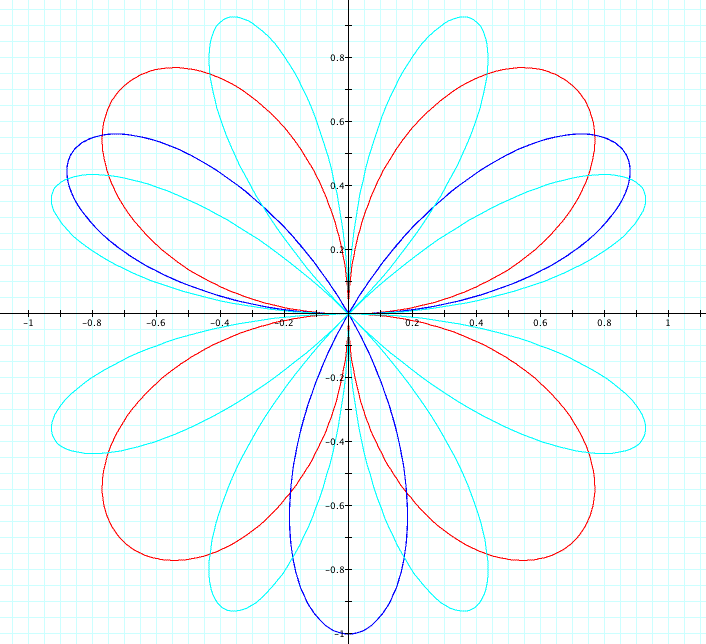
We can see from the graphs that when sine replaces cosine, the graph rotates 90 degrees. Also we can see that when the graph changes to sine, there are 2k petals on the graph, when k is even. When k is odd, there are k number of petals. That does not happen with cosine, just sine.
By Carolyn Amos