

Given triangle ABC. Construct the orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully. Prove that
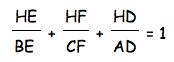
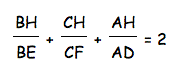
First lets look at the triangle and the measurements of each of the segments and ratios. The measurements alone are not enough for a proof, but at least we will know if the equations hold and that it works for this triangle.
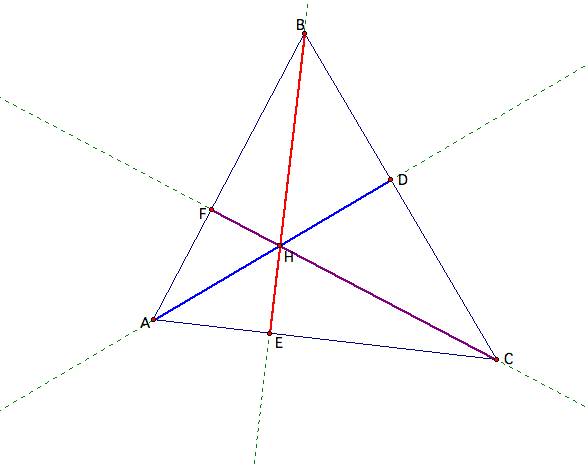

It seems to work just looking at the graph and the measurements given. Click the link to open GSP and play around with the triangle yourself.
Let's take a closer look at the triangle. Triangles HAC, HBA and HCB are all contained in triangle ABC. Therefore triangle ABC is made up of the three small triangles. We know that for all polygons, that the area of the polygon is equal to the sum of the parts which make up the polygon. Therefore the area of triangle ABC is made up of the area of triangles HAC, HBA and HCB. Therefore, we know that
To get the 1 needed on the left side, I will divide the whole equation by Area(ABC), giving
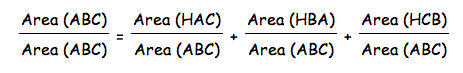
Now I can substitute in the formulas for the area of a triangle.
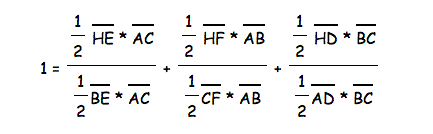
By reducing all the fractions in the above equation, you are left with:
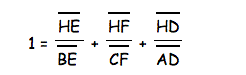
The above equation is the one we were looking for and so we have proved it.
Now we need to show that the following equation is also true.
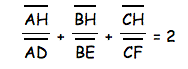
First we start with the previous equation that we proved and then we need to manipulate the numerators a little bit using addition and subtraction of segments. So we can write the numerators as below:
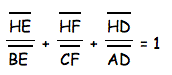
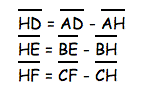
Then we can combine the two, giving:
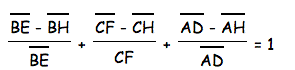
Then we can break up each part of the numerator and put it over the denominator seperately, like below:
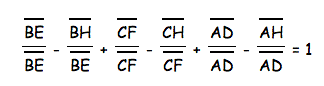
We know that we can change the terms that are the same segment over the same segment into 1. Therefore
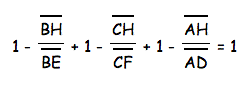
Then we can combine like terms.
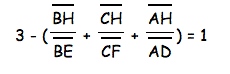
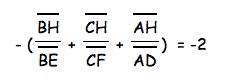
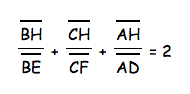
Therefore we see that the equation holds as well.
What happens if the triangle is obtuse?
If the triangle is obtuse, then the only line left within the triangle is segment AD. Both BE and FC disappear when the angle is moved from acute to obtuse. Therefore the equations only apply to acute triangles, not obtuse.
By Carolyn Amos