We are going to examine lots of different constructs of pedal triangles.
First, we should define what a pedal triangle.
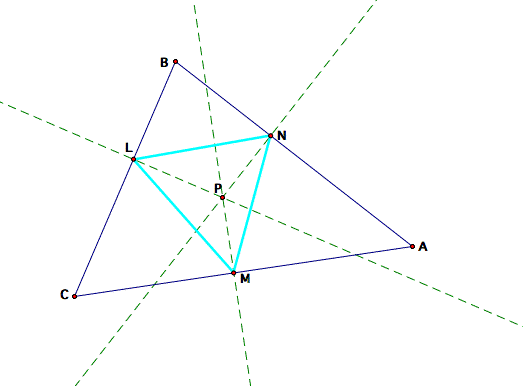
A pedal triangle is obtained by projecting a point onto the sides of a triangle. Consider a triangle ABC and a point, P, that is not one of the vertices. Then you drop perpendiculars from P to the three sides of the triangle. Label the intersections of the lines from P as L, M, N with the sides BC, AC, AB. The pedal triangle is then LMN. See below.

As you can see, the pedal point is inside the triangle and so is the pedal triangle.
What if the pedal point is outside the original triangle?
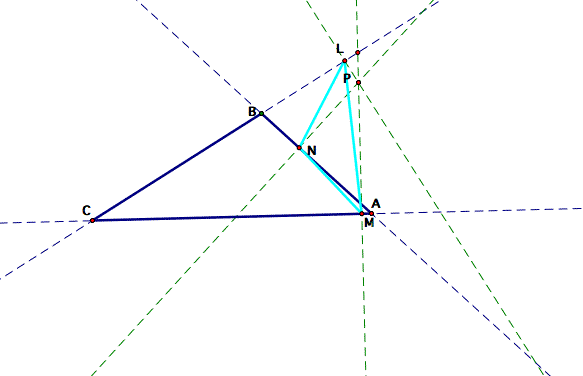
Click here to explore moving around the pedal point and to see what happens when you do.
Now we are going to look at a few specific cases. What will happen if the pedal point is the incenter or the orthocenter or the circumcenter or the centroid?
What happens when the pedal point is the centroid of the triangle? We know that since the centroid is always inside the triangle, that the pedal point will also be inside the triangle, and therefore the pedal triangle will be inside the original triangle.
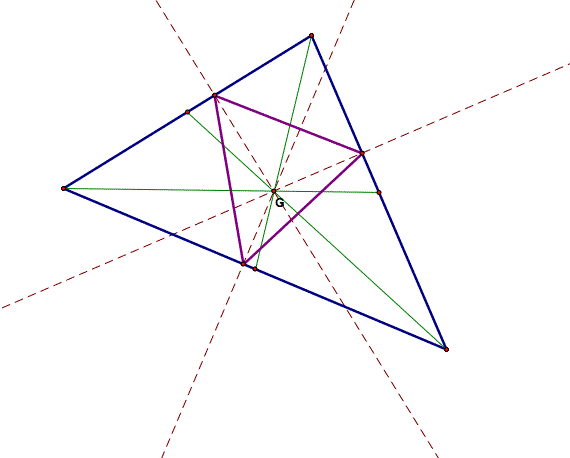
As you can see, the medians of the original triangle hit the pedal point of the triangle. The size of the pedal triangle will always depend upon the size of the original triangle.
Click here to explore what happens when you move the vertices of the triangle.
Let's see what happens when P is the incenter? The incenter is the point where the angle bisectors intersect.
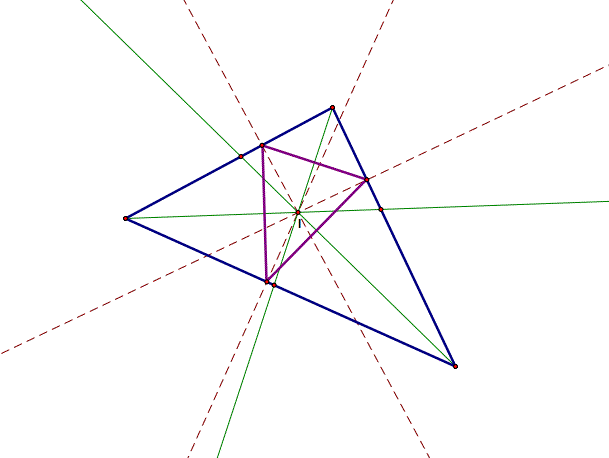
As you can see, the pedal triangle is also inside the triangle. The angle bisectors also intersect the pedal point. In this situation, the pedal triangle is also known as the intouch triangle. The intouch triangle, also known as the contact triangle, is the triangle formed by the points of tangency of the incircle of the original triangle.
Click here to explore what happens when you move the vertices of the triangle.
What about when the pedal point is the orthocenter? The orthocenter is the intersection of the altitudes of the triangle. If you connect the points where they intersect the sides of the original triangle, then you are forming the orthic triangle.
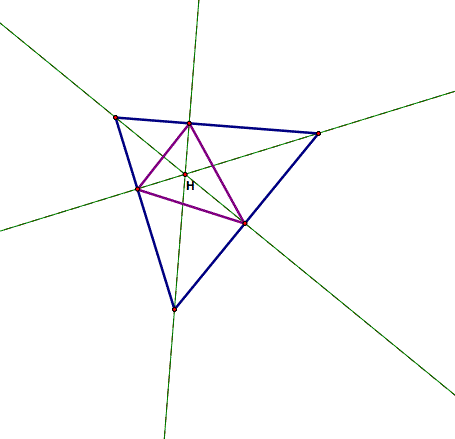
As you can see, the altitudes of the triangle When we find the orthocenter of a triangle and connect the intersections of the altitudes and the sides, then we are finding the pedal triangle. But that is also how you find the orthic triangle, therefore the pedal triangle and the orthic triangle are the same thing when you use the orthocenter as the pedal point. If you explore you will see that when you move the orthocenter outside of the triangle, the pedal triangle disappears.
Click here to explore what happens when you move the vertices of the triangle.
What about when you use the circumcenter as your pedal point? The circumcenter is the intersection of the perpendicular bisectors of the sides of the triangle.
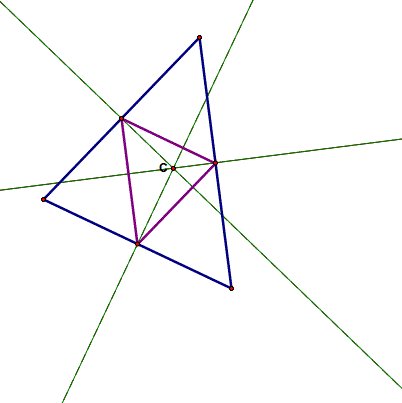
Even though the circumcenter can move outside the triangle, the pedal triangle will always remain inside the triangle. When you use the circumcenter as your pedal point, the pedal triangle is also the medial triangle.
Click here to explore what happens when you move the vertices of the triangle.
By Carolyn Amos