

I wish to find two quadratic functions f(x) and g(x) such that their product h(x) = f(x) * g(x) is tangent to each of f(x) and g(x) at two different points. Since the product of two quadratic functions is a fourth degree polynomial, it may help to first investigate fourth degree functions.
The equations of the curves in the graph below are given as follows:
purple graph = ![]()
green graph =![]()
light blue = ![]()
red graph = ![]()
blue graph =![]()
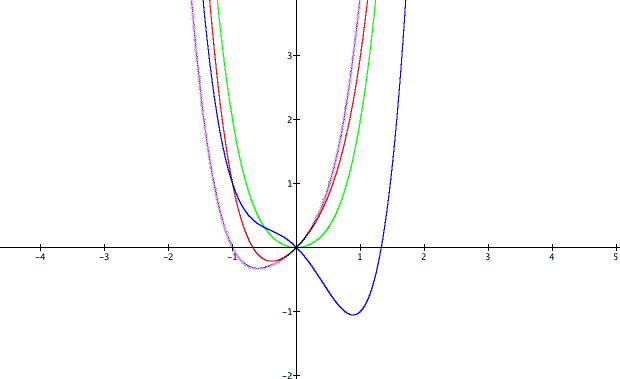
Notice that any functions with odd degree terms
(positive or negative) are asymmetric. While there may exist asymmetric
functions, f(x) and g(x) satisfying the above criteria, it will
be convenient to first explore symmetric choices for these functions.
(It can actually be proven that there exists no functions satisfying
the above criteria, if h(x) is asymmetric, though this proof is
outside the scope of this assignment).
Due to the mentioned symmetry constraints, there are not many choices to check. f(x) must be something of the form ax^0 - x^2 and g(x) of the form x^2 - bx^0.
The first solution I found is given below.
The purple curve is the function ![]() = f(x)
= f(x)
The red curve is ![]() = h(x)
= h(x)
The black curve is f(x) * g(x)
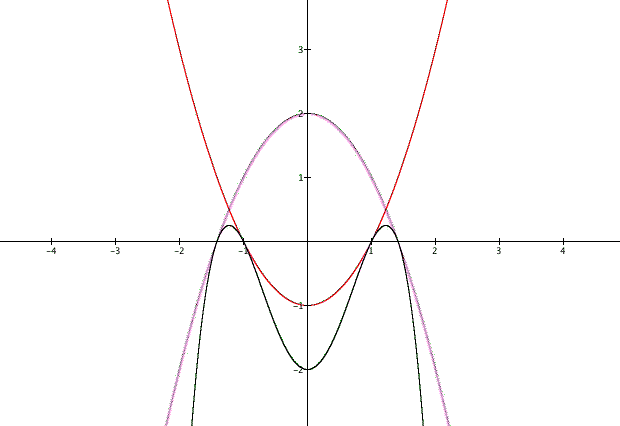
It is interesting to observe the behavior of this solution. One parabola 'contains' h(x), while the other is 'contained' in the trough of h(x).
A second solution is f(x) = 3-x^2, g(x) = x^2-2.
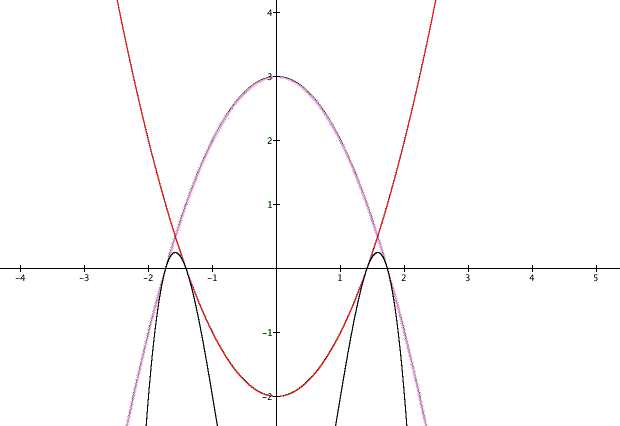
This solution has similar structure to the previous one.
In general, there are infinitely many solutions of the form (a-x^2) = f(x) and g(x) = x^2-b , where a - 1 = b