

This write-up contains results of graphing various parametric equations. The first picture contains three graphs that were the initial assignment graphs designed to demonstrate basic functions of parametric graphing.
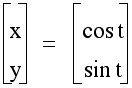 =
red
=
red
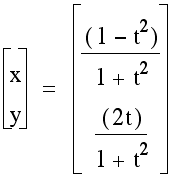 =
yellow
=
yellow
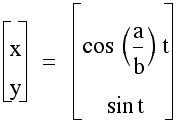 =
purple
=
purple
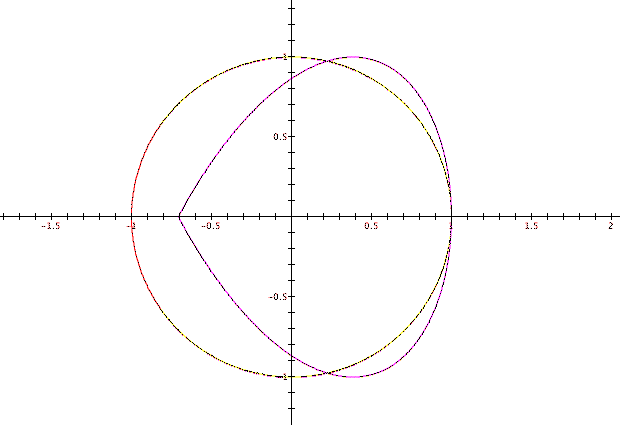
There is nothing too fancy about the results of these graphs, but it is important for students to investigate how slight modfications to the above equations will affect the resulting graphs.
To explore the graphing calculator
file that created these images, click here: Introparametric
There is a particular interesting family of curves, known as the Lisajous curves, which are defined by certain trigonometric expressions, given below. These graphs are interesting in that the values of a and b determine the number of places that the graph crosses the x and y axes, respectively. Can you determine what values of a and b were used to generate the graph below? Try using the linked file!
To explore a graphing calculator
file, click here: Lissajous
Finally, parametric graphing can produce some quite remarkable, aesthetically pleasing results. The equations below involve transcendental, trigonometric, and exponential functions arranged in a non-intuitive manner. However, the result produces a lovely picture of a butterfly!
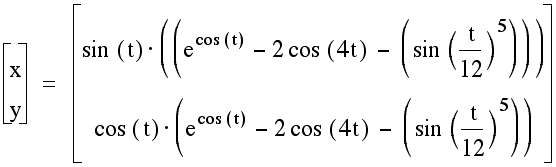
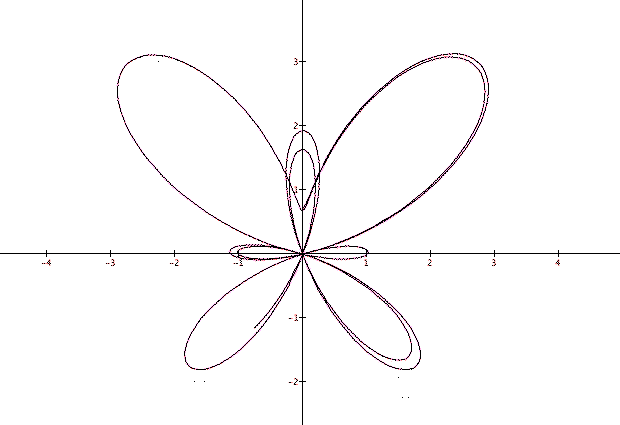
To explore a graphing calculator
file, click here: Butterfly
Parametric graphing is a fun
exploration due to the fact that results can be artistically pleasing,
and the fact that parametric equations are hardly intuitive, even
for the best mathematicians.