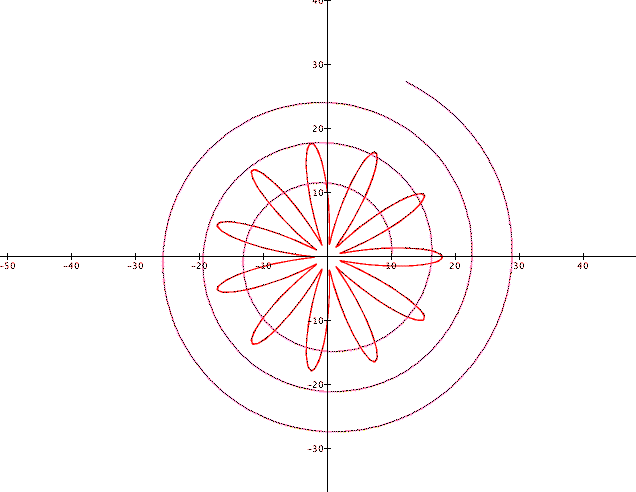
This write-up explores two famous examples of polar equations.
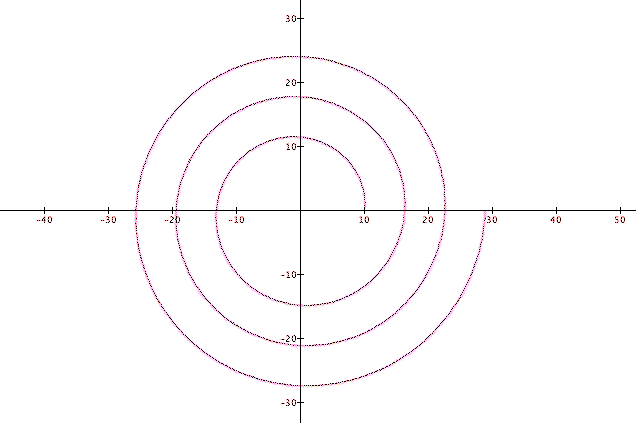
The first equation is known as the spiral of Archimedes. Archimedes surely did not have access to the graphing program that generated the picture below, so it is interesting to think of how he discovered this graph, and whether or not he had conceived of polar coordinates.
![]()
![]()
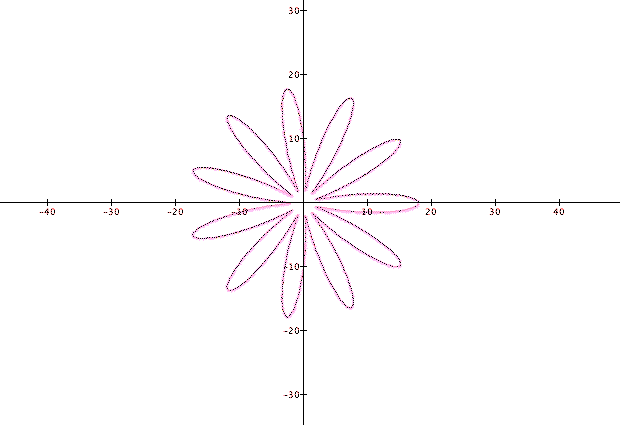
The above image is generated from the given function using the particular values a=10, b=8, k=11. If k is an odd integer, (as in this case) this equation will produce a 'rose' with k petals or a rose with 2k petals if k is an even integer. If k is a rational number but not an integer, the rose may form but with overlapping petals. It is noteworthy that these equations never produce a rose with n petals, where n is a number equivalent to 2 (mod 4), ie 6, 10, 14 etc.
Flowers at the (north?) pole!