

The table at the bottom of this page contains values of the Fibonacci (1st column) and Lucas (3rd column) sequences. The Fibonacci sequence is a sequence where the first two values are equal to one, and each successive term is defined recursively, namely the sum of the two previous terms. The Lucas sequence is similar, though the first term is one and the second term is three, but defined equivalently with the Fibonacci sequence thereafter.
The entries in the second and fourth columns are the ratios of the two preceding terms in the respective sequence. These entries appear to approach the same number, which would be the limit of the ratio of the terms. I will prove that there is such a limit, and give the value of this number.
To consider the limit of the Fibonacci sequence, let
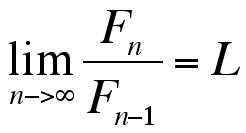
by the properties of limits,
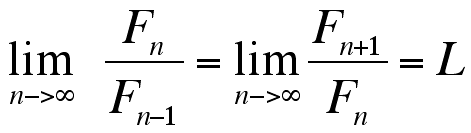
It will be helpful to explicitly state the construction of the Fibonacci sequence to manipulate the above expressions:
![]()
Using this equation to substitute, we get
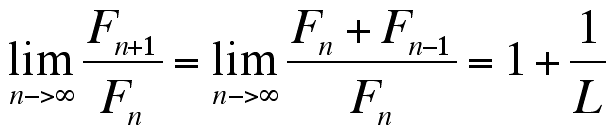
and so we get the equivalent equations
![]()
and finally solving for L using the quadratic formula yields:
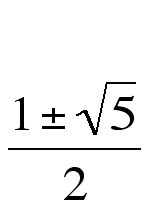
which is the limit of the ratio of the terms, and is approximately 1.618034
As a fun fact, the explicit formula of the Fibonacci sequence is:
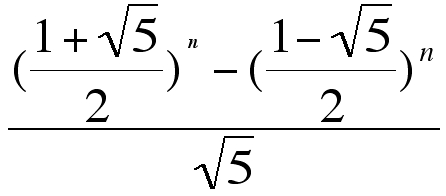
This table confirms the above calculations.
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 3 | 3 | |
| 2 | 2 | 4 | 1.33333333333333 | |
| 3 | 1.5 | 7 | 1.75 | |
| 5 | 1.66666666666667 | 11 | 1.57142857142857 | |
| 8 | 1.6 | 18 | 1.63636363636364 | |
| 13 | 1.625 | 29 | 1.61111111111111 | |
| 21 | 1.61538461538462 | 47 | 1.62068965517241 | |
| 34 | 1.61904761904762 | 76 | 1.61702127659574 | |
| 55 | 1.61764705882353 | 123 | 1.61842105263158 | |
| 89 | 1.61818181818182 | 199 | 1.61788617886179 | |
| 144 | 1.61797752808989 | 322 | 1.61809045226131 | |
| 233 | 1.61805555555556 | 521 | 1.61801242236025 | |
| 377 | 1.61802575107296 | 843 | 1.61804222648752 | |
| 610 | 1.61803713527851 | 1364 | 1.61803084223013 | |
| 987 | 1.61803278688525 | 2207 | 1.61803519061584 | |
| 1597 | 1.61803444782168 | 3571 | 1.6180335296783 | |
| 2584 | 1.61803381340013 | 5778 | 1.61803416409969 | |
| 4181 | 1.61803405572755 | 9349 | 1.61803392177224 | |
| 6765 | 1.61803396316671 | 15127 | 1.61803401433308 | |
| 10946 | 1.6180339985218 | 24476 | 1.61803397897799 | |
| 17711 | 1.61803398501736 | 39603 | 1.61803399248243 | |
| 28657 | 1.6180339901756 | 64079 | 1.61803398732419 | |
| 46368 | 1.61803398820532 | 103682 | 1.61803398929446 | |
| 75025 | 1.6180339889579 | 167761 | 1.61803398854189 | |
| 121393 | 1.61803398867044 | 271443 | 1.61803398882935 | |
| 196418 | 1.61803398878024 | 439204 | 1.61803398871955 | |
| 317811 | 1.6180339887383 | 710647 | 1.61803398876149 | |
| 514229 | 1.61803398875432 | 1149851 | 1.61803398874547 | |
| 832040 | 1.6180339887482 | 1860498 | 1.61803398875159 | |
| 1346269 | 1.61803398875054 | 3010349 | 1.61803398874925 | |
| 2178309 | 1.61803398874965 | 4870847 | 1.61803398875014 | |
| 3524578 | 1.61803398874999 | 7881196 | 1.6180339887498 | |
| 5702887 | 1.61803398874986 | 12752043 | 1.61803398874993 | |
| 9227465 | 1.61803398874991 | 20633239 | 1.61803398874988 | |
| 14930352 | 1.61803398874989 | 33385282 | 1.6180339887499 | |
| 24157817 | 1.6180339887499 | 54018521 | 1.61803398874989 | |
| 39088169 | 1.61803398874989 | 87403803 | 1.6180339887499 | |
| 63245986 | 1.6180339887499 | 141422324 | 1.61803398874989 | |
| 102334155 | 1.61803398874989 | 228826127 | 1.61803398874989 |