

The particular problem is an investigation of eliptical graphs.
We are first required to graph ![]() and
and
![]()
and subsequently explore similar elliptical graphs, with varying xy term.
The picture below shows the graph for
![]() ,
,
where a takes integer values from -4 to 4.
It is interesting to note that there are particular values of a that reduce the ellipse to a line, namely a = 2 or -2. This connection should be demonstrated to students, as the case reduces to a factorable quadratic which gives the equations x+y = 3 and x+y = -3. This particular limiting behavior was one of the key observations that students should see in a problem.
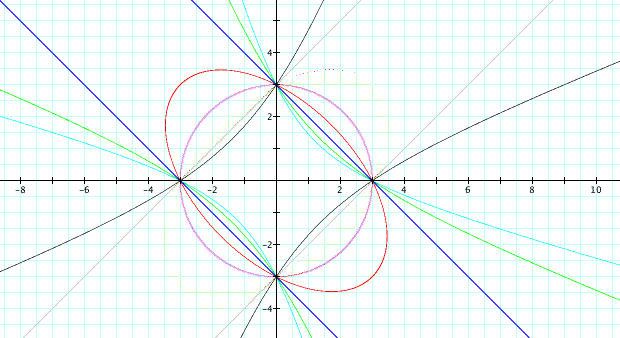
When taking the product of two trigonometric values for the xy term, the graph is (perhaps surprisingly) rather 'normal', creating graphs similar to circles. Some explorations are given below. Trigonometric values are of the product xy are demonstrated in the penultimate graph, and are somewhat more 'exciting'.
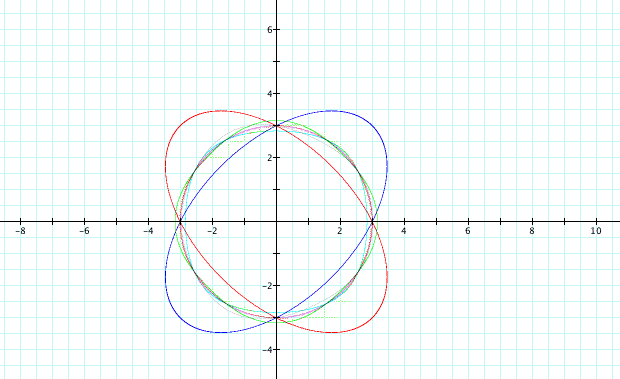
I decided to do some extra exploration, using transcendental and other 'strange' functions. I don't have much commentary other than explicitly stating that the results were indeed 'strange' as predicted.
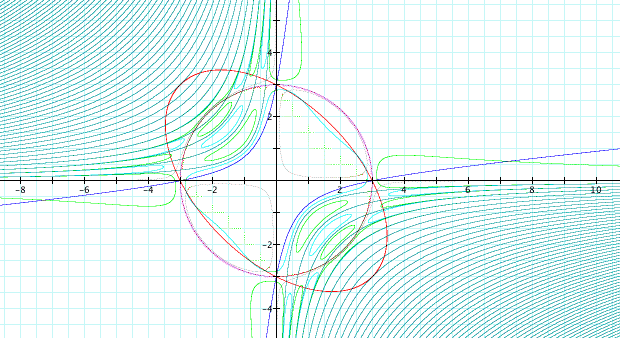
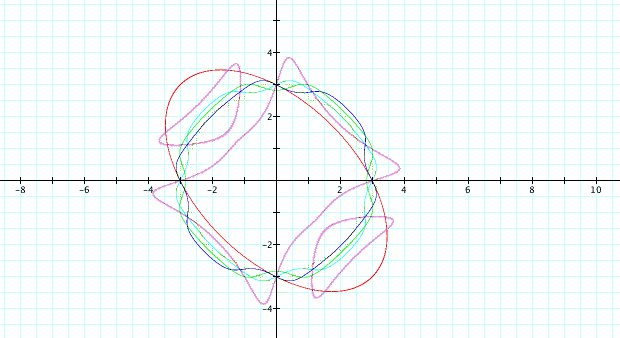
Ellipses are a fascinating topic, and student explorations in this area can be both entertaining as well as rigorously academic. For instance, students can be asked to find an equation that creates a shape close to that of a chicken egg.
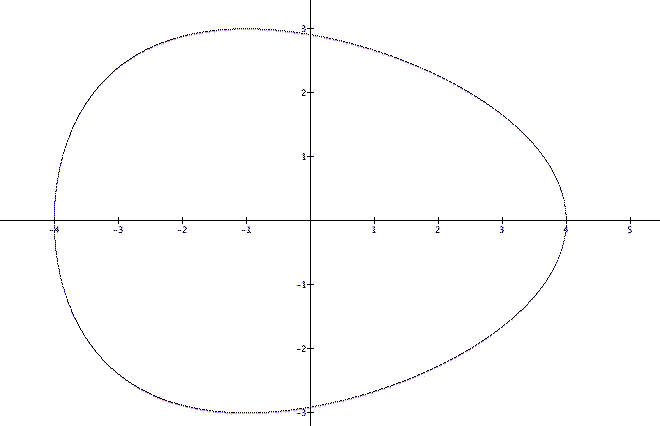
Through scaffolded instruction with hints and
suggestions, the students can arrive at a number of solutions.
This particular egg was generated by :![]()